题目内容
已知等差数列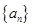 的前
的前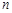 项和为
项和为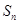 .
.
(1)请写出数列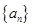 的前
的前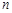 项和
项和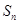 公式,并推导其公式;
公式,并推导其公式;
(2)若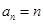 ,数列
,数列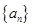 的前
的前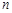 项和为
项和为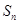 ,求
,求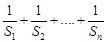 的和.
的和.
(1)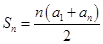 ;(2)
;(2)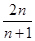 .
.
解析试题分析:(1)推导等差数列前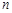 项和
项和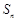 公式的方法比较多,这里介绍一种方法是倒序求和法:所以
公式的方法比较多,这里介绍一种方法是倒序求和法:所以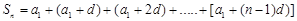 ① ;
① ;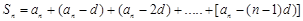 ②,然后利用①②式子之和可得
②,然后利用①②式子之和可得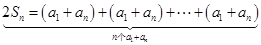
 ,那么有
,那么有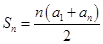 ;(2)因为
;(2)因为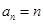 ,所以
,所以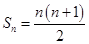 ,那么注意到式子
,那么注意到式子 ,将各项代入后有:
,将各项代入后有: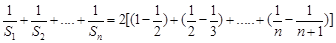
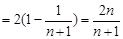 .
.
试题解析:(1)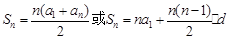 (注:只要写对其中一个公式即可)
(注:只要写对其中一个公式即可)
证明:设等差数列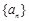 的公差为
的公差为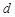 ,因为
,因为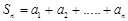
所以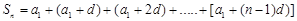 ①
① 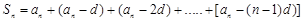 ②
②
由①+②得: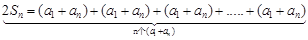

所以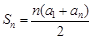
(2)因为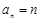 ,所以
,所以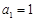 ,
,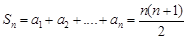
所以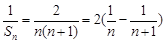
因此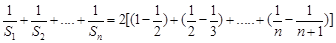
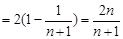 .
.
考点:等差数列;数列求和.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 是等差数列,首项
是等差数列,首项 ,前
,前 项和为
项和为 .令
.令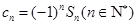 ,
, 的前
的前 项和
项和 .数列
.数列 是公比为
是公比为 的等比数列,前
的等比数列,前 ,且
,且 ,
, .
. 的通项公式;
的通项公式;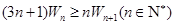 .
.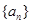 中,
中,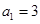 ,其前n项和为
,其前n项和为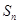 ,等比数列
,等比数列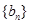 的各项均为正数,
的各项均为正数,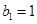 ,公比为q,且
,公比为q,且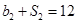 ,
,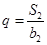 .
.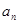 与
与 ;
;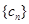 满足
满足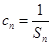 ,求
,求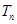 .
.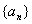 的首项
的首项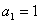 ,前
,前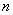 项和为
项和为 (
(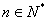 ),且点
),且点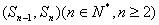 在直线
在直线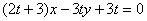 上(
上(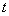 为与
为与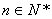 )为等比数列;
)为等比数列;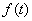 ,数列
,数列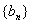 满足
满足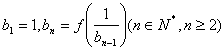 ,设
,设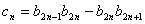 ,求数列
,求数列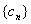 的前
的前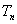 ;
;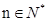 时不等式
时不等式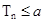 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。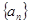 和等比数列
和等比数列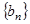 中,
中,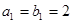 ,
,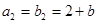 ,
,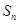 是
是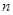 项和.
项和.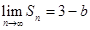 ,求实数
,求实数 的值;
的值;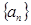 中?若存在,求出所有的
中?若存在,求出所有的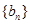 中至少有三项在数列
中至少有三项在数列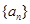 中,但
中,但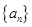 的前
的前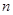 项和为
项和为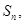 记
记
 的等差数列,求
的等差数列,求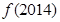 ;
;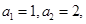 且数列
且数列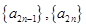 均是公比为
均是公比为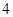 的等比数列,
的等比数列,