题目内容
已知数列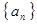 ,满足
,满足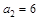 ,
,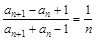
 ,
,
(1)已知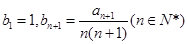 ,求数列
,求数列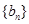 所满足的通项公式;
所满足的通项公式;
(2)求数列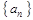 的通项公式;
的通项公式;
(3)己知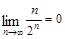 ,设
,设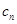 =
=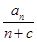
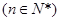 ,常数
,常数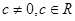 ,若数列
,若数列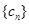 是等差数列,记
是等差数列,记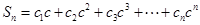 ,求
,求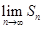 .
.
(1)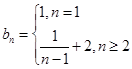 ;(2)
;(2)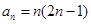 ;(3)
;(3)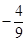 .
.
解析试题分析:(1)这属于数列的综合问题,我们只能从已知条件出发进行推理,以向结论靠拢,由已知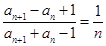 可得
可得 ,从而当
,从而当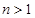 时有结论
时有结论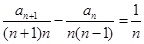
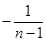 ,很幸运,此式左边正好是
,很幸运,此式左边正好是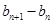 ,则此我们得到了数列
,则此我们得到了数列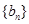 的相邻两项的差
的相邻两项的差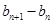 ,那么为了求
,那么为了求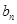 ,可以采取累加的方法(也可引进新数列)求得,注意这里有
,可以采取累加的方法(也可引进新数列)求得,注意这里有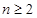 ,对
,对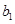 要另外求得;(2)有了第(1)小题
要另外求得;(2)有了第(1)小题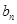 ,那么求
,那么求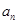 就方便多了,因为
就方便多了,因为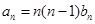 ,这里不再累赘不;(3)在(2)基础上有
,这里不再累赘不;(3)在(2)基础上有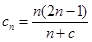 ,我们只有求出
,我们只有求出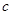 才能求出
才能求出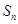 ,这里可利用等差数列的性质,其通项公式为
,这里可利用等差数列的性质,其通项公式为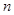 的一次函数(当然也可用等差数列的定义)求出
的一次函数(当然也可用等差数列的定义)求出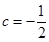 ,从而得到
,从而得到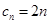 ,那么和
,那么和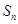 的求法大家应该知道是乘公比错位相减法,借助已知极限
的求法大家应该知道是乘公比错位相减法,借助已知极限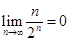 可求出极限
可求出极限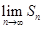 .
.
试题解析:(1)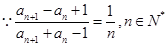 ,
,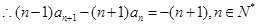 .
.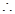 当
当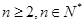 时,有
时,有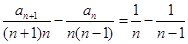 .
.
又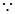
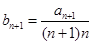 ,
,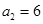 ,
,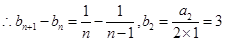 .
.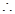 数列
数列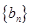 的递推公式是
的递推公式是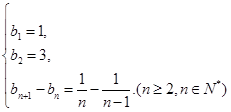 .
.
于是,有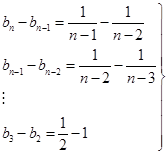
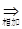
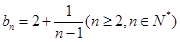 .
.
∴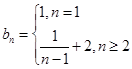 .
.
(说明:这里也可利用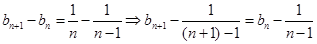 ,依据递推,得
,依据递推,得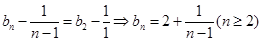 )
)
由(1)得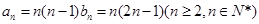 ,
,
又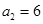 ,可求得
,可求得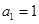 .
.
当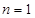 时,
时, ,符合公式
,符合公式 .
. 数列
数列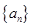 的通项公式
的通项公式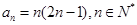 .
.
(3)由(2)知,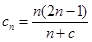 ,
,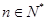 .又
.又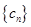 是等差数列,
是等差数列,
因此,当且仅当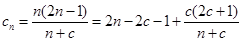 是关于
是关于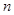 的一次函数或常值函数,即
的一次函数或常值函数,即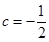 (
(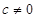 ).
).
于是,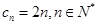 ,
,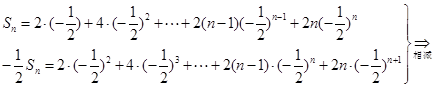
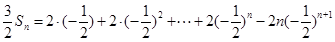 ,
,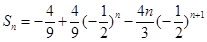 .
.
所以,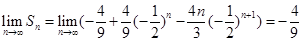 .
.
考点:(1)数列综合题与通项公式;(2)数列通项公式;(3)等差数列的性质,借位相减法,极限.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
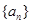 中,
中,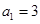 ,其前n项和为
,其前n项和为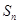 ,等比数列
,等比数列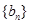 的各项均为正数,
的各项均为正数,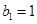 ,公比为q,且
,公比为q,且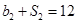 ,
,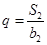 .
.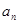 与
与 ;
;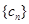 满足
满足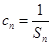 ,求
,求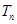 .
.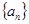 的各项均为正数,且
的各项均为正数,且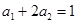 ,
,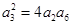 .
.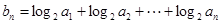 ,求数列
,求数列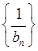 的前
的前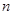 项和.
项和.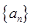 、
、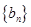 的每一项都是正数,
的每一项都是正数,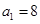 ,
,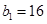 ,且
,且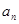 、
、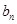 、
、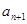 成等差数列,
成等差数列,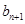 成等比数列,
成等比数列,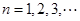 .
.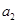 、
、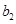 的值;
的值; ,有
,有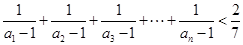 .
. 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.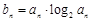 ,求数列{bn}的前n项和
,求数列{bn}的前n项和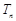 .
.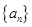 的前
的前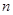 项和为
项和为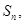 记
记
 的等差数列,求
的等差数列,求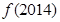 ;
;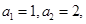 且数列
且数列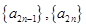 均是公比为
均是公比为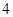 的等比数列,
的等比数列,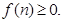
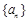 中,前n项和为
中,前n项和为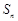 ,且
,且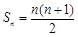 .
.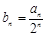 ,数列
,数列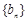 前n项和为
前n项和为 ,求
,求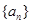 是公差大于零的等差数列,已知
是公差大于零的等差数列,已知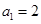 ,
,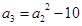 .
.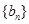 是以函数
是以函数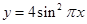 的最小正周期为首项,以
的最小正周期为首项,以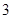 为公比的等比数列,求数列
为公比的等比数列,求数列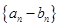 的前
的前 项和
项和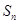 .
.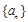 前三项的和为
前三项的和为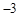 ,前三项的积为
,前三项的积为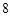 .
.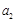 ,
,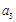 ,
,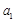 成等比数列,求数列
成等比数列,求数列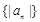 的前
的前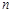 项和.
项和.