题目内容
已知数列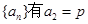 (常数
(常数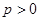 ),其前
),其前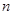 项和为
项和为
 (
(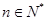 )
)
(1)求数列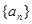 的首项
的首项 ,并判断
,并判断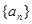 是否为等差数列,若是求其通项公式,不是,说明理由;
是否为等差数列,若是求其通项公式,不是,说明理由;
(2)令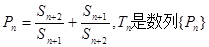 的前n项和,求证:
的前n项和,求证: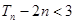
(1) 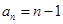 (2)证明过程详见解析
(2)证明过程详见解析
解析试题分析:
(1)当n=1,利用 带入
带入 即可得到
即可得到 的值.当
的值.当 时,利用
时,利用 ,整理可得到
,整理可得到 ,再用叠乘法即可求出
,再用叠乘法即可求出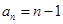 ,即可证明
,即可证明 是等比数列.
是等比数列.
(2)由(2)得到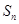 ,带入
,带入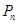 即可得到通项公式
即可得到通项公式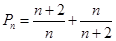 ,考虑利用裂项求和得到
,考虑利用裂项求和得到 (即分离分母即可得到
(即分离分母即可得到 ),即可得到
),即可得到 .再利用
.再利用 ,即可证明
,即可证明 .
.
试题解析:
(1)当n=1时, ,则
,则 ……①
……①
当 时,
时, ……②,
……②,
则①-②得

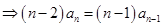
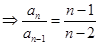
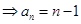 ,
,
检验n=1时也符合,故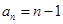 ,则
,则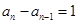 ,所以
,所以 为等差数列.综上
为等差数列.综上 是等差数列且
是等差数列且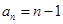 .
.
(2)由(1)
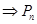

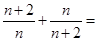
 ,
,
则
 ,
,
所以 ,因为
,因为 且
且 ,所以
,所以 .
.
考点:等差数列 前n项和 裂项求和

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
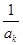 ,
,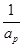 ,
,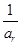 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.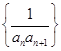 的前n项和,若Tn≤
的前n项和,若Tn≤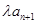 ¨对
¨对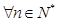 恒成立,求实数
恒成立,求实数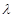 的最小值.
的最小值. 是等差数列,首项
是等差数列,首项 ,前
,前 项和为
项和为 .令
.令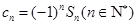 ,
, 的前
的前 项和
项和 .数列
.数列 是公比为
是公比为 的等比数列,前
的等比数列,前 ,且
,且 ,
, .
. 的通项公式;
的通项公式;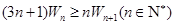 .
.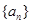 中,
中,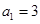 ,其前n项和为
,其前n项和为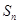 ,等比数列
,等比数列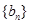 的各项均为正数,
的各项均为正数,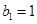 ,公比为q,且
,公比为q,且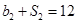 ,
,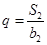 .
.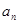 与
与 ;
;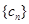 满足
满足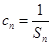 ,求
,求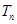 .
.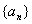 的首项
的首项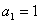 ,前
,前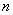 项和为
项和为 (
(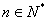 ),且点
),且点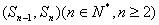 在直线
在直线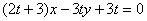 上(
上(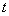 为与
为与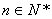 )为等比数列;
)为等比数列;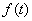 ,数列
,数列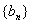 满足
满足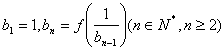 ,设
,设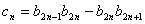 ,求数列
,求数列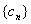 的前
的前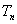 ;
;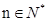 时不等式
时不等式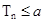 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。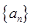 、
、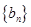 的每一项都是正数,
的每一项都是正数,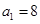 ,
,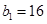 ,且
,且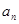 、
、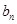 、
、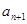 成等差数列,
成等差数列,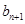 成等比数列,
成等比数列,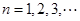 .
.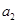 、
、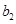 的值;
的值; ,有
,有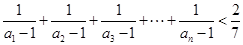 .
.