题目内容
已知圆 的圆心为抛物线
的圆心为抛物线 的焦点,且与直线
的焦点,且与直线 相切,则该圆的方程为( )
相切,则该圆的方程为( )
A. | B. |
C. | D. |
C
解析试题分析:易知抛物线 的焦点为(1,0),所以
的焦点为(1,0),所以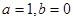 ,又因为圆与直线
,又因为圆与直线 相切,所以
相切,所以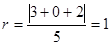 ,所以圆的方程为
,所以圆的方程为 。
。
考点:抛物线的简单性质;圆的简单性质;点到之线的距离公式。
点评:要求圆的方程,确定圆心坐标与半径是关键.

练习册系列答案
相关题目
若点P(3,-1)为圆 的弦AB的中点,则直线AB的方程为( )
的弦AB的中点,则直线AB的方程为( )
| A.x+y-2=0 | B.2x-y-7=0 | C.2x+y-5=0 | D.x-y-4=0 |
若圆 :
: 关于直线
关于直线 对称,则
对称,则 的最小值是( )
的最小值是( )
| A.2 | B. | C. | D. |
点 在圆
在圆 内,则直线
内,则直线 和已知圆的公共点个数为
和已知圆的公共点个数为
| A.0 | B.1 | C.2 | D.不能确定 |
过原点且倾斜角为 的直线被圆学
的直线被圆学 所截得的弦长为
所截得的弦长为
A. | B.2 | C. | D.2 |
若直线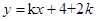 与曲线
与曲线 有两个交点,则
有两个交点,则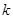 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知焦点在 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是( )
的半径,则椭圆的标准方程是( )
A. | B. | C. | D. |
过点 作直线
作直线 与圆
与圆 相交于
相交于 两点,那么
两点,那么 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
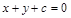 上,则点(m,c)不满足下列哪个方程( )
上,则点(m,c)不满足下列哪个方程( )


