题目内容
【题目】若函数
有四个零点,则实数
的取值范围是____．
【答案】
【解析】由f（x）=0得x2（x﹣4）2=a|x﹣2|﹣2a，
作出y=x2（x﹣4）2与y=a|x﹣2|﹣2a的函数图象，如图所示：
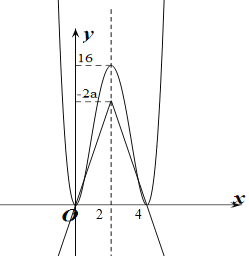
∵f（x）有4个零点，且两函数图象均关于直线x=2对称，
∴y=x2（x﹣4）2与y=a|x﹣2|﹣2a的函数图象在（2，+∞）上有两个交点，
∵两函数图象都经过点（4，0），
∴0＜﹣2a＜16，或﹣2a＜0，或直线y=a（x﹣2）﹣2a与y=x2（x﹣4）2相切，
若0＜﹣2a＜16，解得﹣8＜a＜0；
若﹣2a＜0，解得a＞0；
若直线y=a（x﹣2）﹣2a与y=x2（x﹣4）2相切，设切点为（x0，y0），
则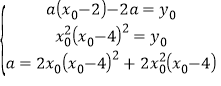
，解得a=﹣
．
故答案为：（﹣8，0）∪（0，+∞）∪{﹣}．
练习册系列答案
相关题目
