题目内容
本题满分14分) 设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为 .若在
.若在 上,有
上,有 恒成立,则称函数
恒成立,则称函数 在
在
 上为“凸函数”.已知
上为“凸函数”.已知 .
.
(Ⅰ) 若 为区间
为区间 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数 的值;
的值;
(Ⅱ) 若当实数 满足
满足 时,函数
时,函数 在
在 上总为“凸函数”,求
上总为“凸函数”,求 的最大值.
的最大值.
【答案】
解:由函数 得,
得, (3分)
(3分)
(Ⅰ) 若 为区间
为区间 上的“凸函数”,则有
上的“凸函数”,则有 在区间
在区间 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当
 ,
,
即
 .
(7分)
.
(7分)
(Ⅱ)当 时,
时, 恒成立
恒成立 当
当 时,
时, 恒成立.
(8分)
恒成立.
(8分)
当 时,
时, 显然成立
(9分)
显然成立
(9分)
当 ,
, ∵
∵ 的最小值是
的最小值是 .∴
.∴ .
.
从而解得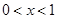 (11分)
(11分)
当 ,
, ∵
∵ 的最大值是
的最大值是 ,∴
,∴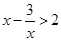 ,
,
从而解得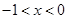 .
.
综上可得 ,从而
,从而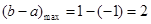 (14分)
(14分)
【解析】略

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。  .
. ,求函数
,求函数 的极值;
的极值; ,试确定
,试确定 的单调性;
的单调性; ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.