题目内容
如图,直线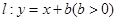 ,抛物线
,抛物线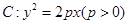 ,已知点
,已知点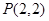 在抛物线
在抛物线 上,且抛物线
上,且抛物线 上的点到直线
上的点到直线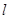 的距离的最小值为
的距离的最小值为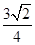 .
.
(1)求直线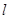 及抛物线
及抛物线 的方程;
的方程;
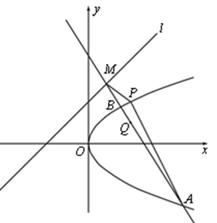
(2)过点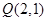 的任一直线(不经过点
的任一直线(不经过点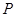 )与抛物线
)与抛物线 交于
交于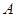 、
、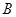 两点,直线
两点,直线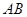 与直线
与直线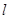 相交于点
相交于点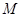 ,记直线
,记直线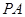 ,
,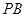 ,
,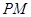 的斜率分别为
的斜率分别为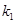 ,
,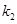 ,
, 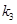 .问:是否存在实数
.问:是否存在实数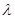 ,使得
,使得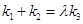 ?若存在,试求出
?若存在,试求出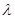 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
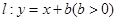 ,抛物线
,抛物线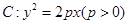 ,已知点
,已知点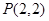 在抛物线
在抛物线 上,且抛物线
上,且抛物线 上的点到直线
上的点到直线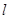 的距离的最小值为
的距离的最小值为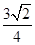 .
.
(1)求直线
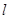 及抛物线
及抛物线 的方程;
的方程;(2)过点
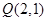 的任一直线(不经过点
的任一直线(不经过点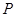 )与抛物线
)与抛物线 交于
交于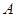 、
、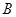 两点,直线
两点,直线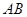 与直线
与直线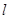 相交于点
相交于点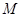 ,记直线
,记直线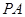 ,
,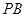 ,
,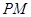 的斜率分别为
的斜率分别为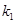 ,
,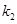 ,
, 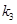 .问:是否存在实数
.问:是否存在实数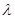 ,使得
,使得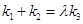 ?若存在,试求出
?若存在,试求出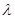 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)直线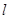 的方程为
的方程为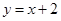 ,抛物线
,抛物线 的方程为
的方程为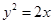 .(2)存在且
.(2)存在且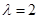
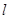 的方程为
的方程为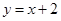 ,抛物线
,抛物线 的方程为
的方程为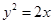 .(2)存在且
.(2)存在且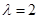
试题分析:
(1)把点P的坐标带入抛物线方程即可求出抛物线方程,而直线l方程的求解有两种方法,法1,可以考虑求出既与抛物线相切,又与直线l平行的直线,该直线与直线l的距离即为抛物线上的点到直线l的最短距离,进而可以求的相应的b值。法二,可以设抛物线上任意一点为
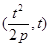 ,列出点
,列出点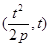 到直线l的距离公式,再利用二次函数的最值即可得到相应的b值。
到直线l的距离公式,再利用二次函数的最值即可得到相应的b值。(2)直线AB经过点Q且不经过P,所以直线AB斜率存在且利用点斜式设出直线方程,联立直线与抛物线方程,得到关于A,B横坐标或者纵坐标的韦达定理,进而利用AB直线的斜率表示PA,PB直线的斜率,再联立直线AB与直线l,用AB直线斜率表示PM直线的斜率,得到
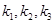 关于AB直线斜率的表达式,带入
关于AB直线斜率的表达式,带入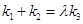 即可求的
即可求的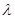 的值.
的值.试题解析:
(1)(法一)
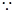 点
点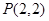 在抛物线
在抛物线 上,
上, 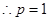 . 2分
. 2分设与直线
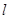 平行且与抛物线
平行且与抛物线 相切的直线
相切的直线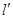 方程为
方程为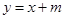 ,
,由
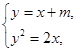 得
得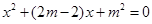 ,
,  ,
,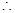 由
由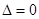 ,得
,得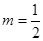 ,则直线
,则直线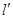 方程为
方程为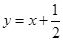 .
.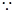 两直线
两直线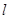 、
、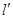 间的距离即为抛物线
间的距离即为抛物线 上的点到直线
上的点到直线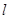 的最短距离,
的最短距离, 有
有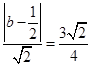 ,解得
,解得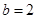 或
或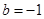 (舍去).
(舍去). 直线
直线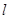 的方程为
的方程为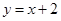 ,抛物线
,抛物线 的方程为
的方程为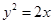 . 6分
. 6分(法二)
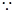 点
点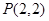 在抛物线
在抛物线 上,
上, 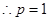 ,抛物线
,抛物线 的方程为
的方程为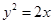 . 2分
. 2分设
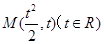 为抛物线
为抛物线 上的任意一点,点
上的任意一点,点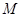 到直线
到直线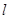 的距离为
的距离为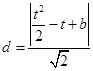 ,根据图象,有
,根据图象,有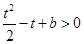 ,
,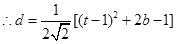 ,
,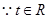 ,
,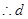 的最小值为
的最小值为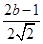 ,由
,由 ,解得
,解得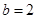 .
.因此,直线
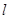 的方程为
的方程为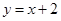 ,抛物线
,抛物线 的方程为
的方程为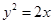 . 6分
. 6分(2)
 直线
直线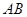 的斜率存在,
的斜率存在, 设直线
设直线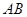 的方程为
的方程为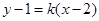 ,即
,即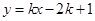 ,
,由
 得
得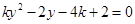 ,
,设点
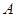 、
、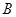 的坐标分别为
的坐标分别为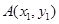 、
、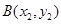 ,则
,则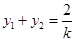 ,
,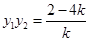 ,
,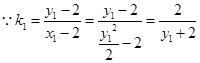 ,
, , 9分
, 9分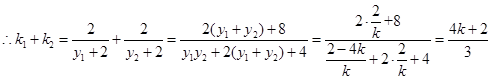 . 10分
. 10分由
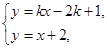 得
得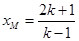 ,
,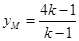 ,
,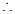
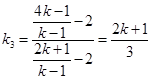 , 13分
, 13分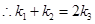 .
.因此,存在实数
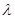 ,使得
,使得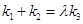 成立,且
成立,且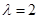 . 14分
. 14分
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
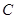 过定点(1,0),且与直线
过定点(1,0),且与直线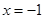 相切.
相切.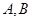 是轨迹
是轨迹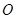 的两个不同点,直线
的两个不同点,直线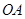 和
和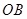 的倾斜角分别为
的倾斜角分别为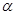 和
和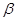 ,①当
,①当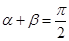 时,求证直线
时,求证直线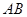 恒过一定点
恒过一定点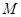 ;
;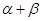 为定值
为定值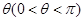 ,直线
,直线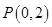 ,抛物线
,抛物线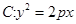
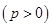 的焦点
的焦点 ,线段
,线段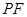 与抛物线
与抛物线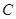 的交点为
的交点为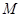 ,过
,过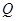 ,若
,若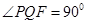 ,则
,则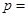 _______.
_______.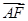 =
=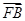 ,
,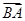 ·
·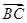 =36,则抛物线的方程为________.
=36,则抛物线的方程为________.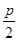 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.