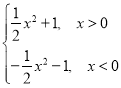题目内容
【题目】判断下列函数的奇偶性：
（1）f(x)＝x＋1；
（2）f(x)＝x3＋3x，x∈[－4，4)；
（3）f(x)＝|x－2|－|x＋2|；
（4）f(x)＝
【答案】（1）既不是奇函数又不是偶函数；（2）既不是奇函数又不是偶函数；（3）奇函数；（4）奇函数.
【解析】
根据函数的奇偶性的定义，结合函数的解析式，逐个判定，即可求解.
（1）函数f(x)＝x＋1的定义域为实数集R，关于原点对称．
因为f(－x)＝－x＋1＝－(x－1)，－f(x)＝－(x＋1)，即f(－x)≠－f(x)，f(－x)≠f(x)，
所以函数f(x)＝x＋1既不是奇函数又不是偶函数．
（2）因为函数的定义域不关于原点对称，即存在－4∈[－4，4)，而4[－4，4)，
所以函数f(x)＝x3＋3x，x∈[－4，4)既不是奇函数又不是偶函数．
（3）函数f(x)＝|x－2|－|x＋2|的定义域为实数集R，关于原点对称．
因为f(－x)＝|－x－2|－|－x＋2|＝|x＋2|－|x－2|＝－(|x－2|－|x＋2|)＝－f(x)，
所以函数f(x)＝|x－2|－|x＋2|是奇函数．
（4）函数的定义域为(－∞，0)∪(0，＋∞)，关于原点对称．
当x>0时，－x<0，f(－x)＝－
(－x)2－1＝－(x2＋1)＝－f(x)；
当x<0时，－x>0，f(－x)＝ (－x)2＋1＝x2＋1＝－(－x2－1)＝－f(x)．
综上可知，函数f(x)＝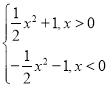
是奇函数．
练习册系列答案
相关题目
【题目】某学校调查了20个班中有网上购物经历的人数，得到了如图所示的茎叶图，以
为分组，作出这组数的频率分布直方图，并说明频率分布直方图与茎叶图之间的关系.
0 1 2 3 | 7 3 7 6 4 4 3 0 7 5 5 4 3 2 0 8 5 4 3 0 |
