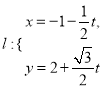题目内容
【题目】已知圆
经过椭圆
的右顶点
、下顶点
和上顶点
．
（1）求圆的标准方程；
（2）直线
经过点
且与
垂直，
是直线上的动点，过点作圆的切线，切点分别为
，求四边形
面积的最小值．
【答案】(1) 
. (2) 
【解析】
（1）根据圆心必在圆上两点连线的中垂线上可知圆心必在
轴上，设圆心
，可得半径
，利用圆心到圆上点的距离等于半径可构造方程求得圆心和半径，从而得到圆的方程；（2）根据两直线垂直可求得直线
的方程，利用
可知当四边形面积最小时，
取最小值；当切线长最小时，
；利用点到直线距离公式和勾股定理可求得的最小值，代入可得面积的最小值.
（1）由椭圆方程得：
，
，
由圆
过
可知：圆心必在轴上
设圆心为，则半径
，解得：
圆心为
，半径
圆的标准方程为：
（2）
直线与
垂直 
直线方程为：
，即：
且
当
取最小值时，最小
又
且当时，最小
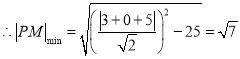
四边形
面积的最小值为：
【题目】甲、乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台机床生产的零件各100件进行检测，检测结果统计如下：
测试指标 | [85，90） | [90，95） | [95，100） | [100，105） | [105，110） |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
（1）试分别估计甲机床、乙机床生产的零件为优品的概率；
（2）甲机床生产1件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元，假设甲机床某天生产50件零件，请估计甲机床该天的利润（单位：元）；
（3）从甲、乙机床生产的零件指标在[90，95）内的零件中，采用分层抽样的方法抽取5件，从这5件中任意抽取2件进行质量分析，求这2件都是乙机床生产的概率.
【题目】下面是某市环保局连续30天对空气质量指数的监测数据：
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
（1）完成下面的频率分布表；
（2）完成下面的频率分布直方图，并写出频率分布直方图中
的值；
（3）在本月空气质量指数大于等于91的这些天中随机选取两天，求这两天中至少有一天空气质量指数在区间
内的概率．
分组 | 频数 | 频率 |
[41，51) | 2 |
|
[51，61) | 3 |
|
[61，71) | 4 |
|
[71，81) | 6 |
|
[81，91) | ||
[91，101) | 3 | |
[101，111) |
|
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关，某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查，调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I) 根据列联表判断，是否有90%的把握认为学生使用手机的时间长短与性别有关;
（II)在参与调查的平均每天使用手机不超过3小时的10名男生中，有6人使用国产手机，从这10名男生中任意选取3人，求这3人中使用国产手机的人数
的分布列和数学期望.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式：
