题目内容
函数 在
在 上的最大值和最小值分别是 ( )
上的最大值和最小值分别是 ( )
A. | B.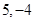 | C.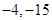 | D.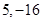 |
A
解析试题分析:由题设知y'=6x2-6x-12,令y'>0,解得x>2,或x<-1,故函数y=2x3-3x2-12x+5在[0,2]上减,在[2,3]上增,当x=0,y=5;当x=3,y=-4;当x=2,y=-15.由此得函数y=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是5,-15,故选A
考点:本题考查了用导数研究函数的单调性求最值
点评:此类问题是导数一章中最基本的题型,常常利用导数法判断函数的单调性,然后求出最值

练习册系列答案
相关题目
用二分法计算函数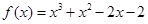 的一个正数零点的近似值(精确到0.1)为( )
的一个正数零点的近似值(精确到0.1)为( )
参考数据:
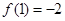 | 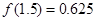 |
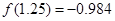 | 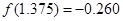 |
 | 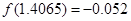 |
下列函数中既是奇函数,又在区间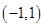 上是增函数的为( )
上是增函数的为( )
A.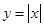 | B.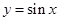 | C.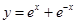 | D.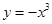 |
已知函数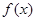 对任意
对任意 都有
都有 ,若
,若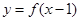 的象关于直线
的象关于直线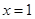 对称,且
对称,且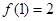 ,则
,则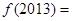 ( )
( )
| A.2 | B.3 | C.4 | D.0 |
已知函数 ,则函数
,则函数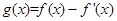 的零点所在的区间是( )
的零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
函数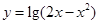 的单调递增区间为( )
的单调递增区间为( )
A.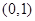 | B.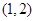 | C.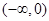 | D.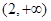 |
若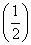 2a+1<
2a+1<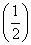 3-2a,则实数a的取值范围是( ).
3-2a,则实数a的取值范围是( ).
| A.(1,+∞) | B.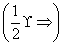 |
| C.(-∞,1) | D.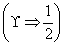 |
 ,观察:
,观察: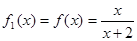 ,
,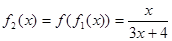 ,,
,, ,
, 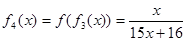 ……根据以上事实,由归纳推理可得当
……根据以上事实,由归纳推理可得当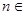 N*且
N*且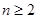 时,
时, 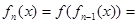 ( )
( )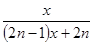
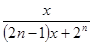
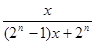
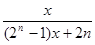
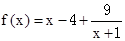 ,
,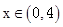 ,当
,当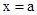 时,
时,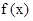 取得最小值
取得最小值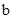 ,则函数
,则函数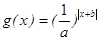 的图象为( )
的图象为( )