题目内容
若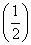 2a+1<
2a+1<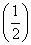 3-2a,则实数a的取值范围是( ).
3-2a,则实数a的取值范围是( ).
| A.(1,+∞) | B.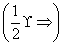 |
| C.(-∞,1) | D.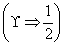 |
B
解析试题分析:函数y=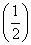 x在R上为减函数,∴2a+1>3-2a,∴a>
x在R上为减函数,∴2a+1>3-2a,∴a>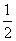 .故选B
.故选B
考点:本题考查了函数单调性的运用
点评:利用指数函数的单调性解含指数的不等式是解决此类问题的关键,属基础题

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
函数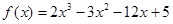 在
在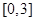 上的最大值和最小值分别是 ( )
上的最大值和最小值分别是 ( )
A.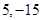 | B.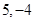 | C.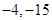 | D.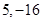 |
下列函数中,在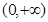 上为增函数的是 ( )
上为增函数的是 ( )
A.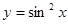 | B. |
C.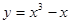 | D.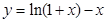 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B. | C. | D. |
函数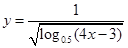 的定义域为( )
的定义域为( )
A.(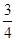 ,1) ,1) | B.(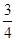 ,+∞) ,+∞) | C.(1,+∞) | D.(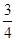 ,1)∪(1,+∞) ,1)∪(1,+∞) |
函数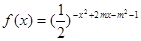 的单调增区间与值域相同,则实数
的单调增区间与值域相同,则实数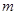 的取
的取
值为( )
A.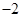 | B.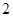 | C.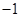 | D.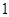 |
偶函数 在
在 上为增函数,若不等式
上为增函数,若不等式 对
对 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为
A. | B. | C. | D. |
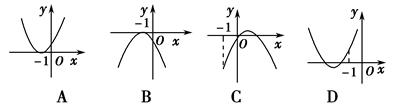
 的图象是
的图象是