题目内容
已知函数 ,则函数
,则函数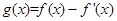 的零点所在的区间是( )
的零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
B
解析试题分析: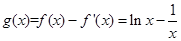 ,易知
,易知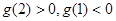 ,所以根据零点存在性定理
,所以根据零点存在性定理 在
在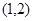 间有零点.
间有零点.
考点:函数零点的判定定理
点评:本题主要考查函数的零点及函数的零点存在性定理,若函数在区间[a,b]上联系且单调,且f(a)•f(b)<0,则函数在区间(a,b)上有唯一零点,体现了函数与方程的思想的应用.

练习册系列答案
相关题目
已知函数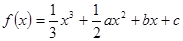 在
在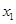 处取得极大值,在
处取得极大值,在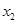 处取得极小值,满足
处取得极小值,满足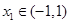 ,
,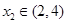 ,则
,则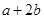 的取值范围是
的取值范围是
A.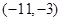 | B.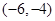 | C.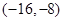 | D.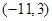 |
设函数 ,则在下列区间中函数
,则在下列区间中函数 不存在零点的是
不存在零点的是
A.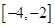 | B.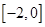 | C.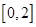 | D.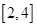 |
函数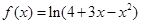 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B.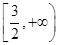 | C.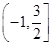 | D.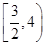 |
函数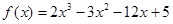 在
在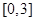 上的最大值和最小值分别是 ( )
上的最大值和最小值分别是 ( )
A.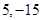 | B.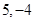 | C.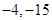 | D.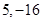 |
下列函数中,既是 上的奇函数,又在
上的奇函数,又在 上单调递增的是( )
上单调递增的是( )
A.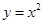 | B.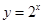 | C.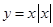 | D.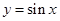 |
已知函数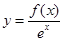 ,满足
,满足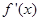 >
> ,则
,则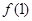 与
与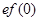 的大小关系是( )
的大小关系是( )
A.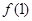 < <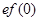 | B.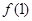 > >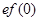 |
C.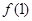 = = 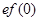 | D.不能确定 |
函数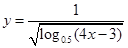 的定义域为( )
的定义域为( )
A.(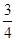 ,1) ,1) | B.(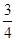 ,+∞) ,+∞) | C.(1,+∞) | D.(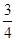 ,1)∪(1,+∞) ,1)∪(1,+∞) |
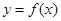 在区间
在区间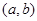 上的导函数为
上的导函数为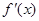 ,
,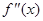 ,若在区间
,若在区间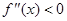 恒成立,则称函数
恒成立,则称函数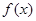 在区间
在区间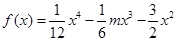 ,若对任意的实数
,若对任意的实数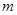 满足
满足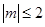 时,函数
时,函数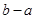 的最大值为
的最大值为