题目内容
设各项均为正数的数列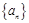 的前n项和为Sn,已知
的前n项和为Sn,已知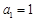 ,且
,且 对一切
对一切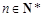 都成立.
都成立.
(1)若λ = 1,求数列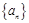 的通项公式;
的通项公式;
(2)求λ的值,使数列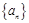 是等差数列.
是等差数列.
(1)an=2n-1(2)λ=0.
解析试题分析:(1)本题属于“已知 求
求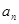 ”,利用
”,利用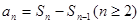 化简关系式. 因为
化简关系式. 因为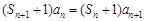 ,所以先分离
,所以先分离 与
与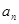 ,即
,即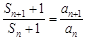 ,这是类等比,利用叠乘法得到
,这是类等比,利用叠乘法得到 ,再利用
,再利用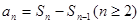 ,消去
,消去 得
得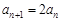 .求数列{an}通项公式时,需讨论当n = 1时是否满足
.求数列{an}通项公式时,需讨论当n = 1时是否满足 的情形.(2)解答本题需注意逻辑关系,由数列
的情形.(2)解答本题需注意逻辑关系,由数列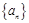 是等差数列得λ = 0,这是一个必要条件,还需验证其充分性,即λ = 0时,数列
是等差数列得λ = 0,这是一个必要条件,还需验证其充分性,即λ = 0时,数列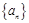 是等差数列.这可类似(1)的解答过程.
是等差数列.这可类似(1)的解答过程.
试题解析:解:(1)若λ = 1,则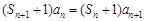 ,
,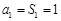 .
.
又∵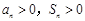 , ∴
, ∴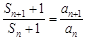 , 2分
, 2分
∴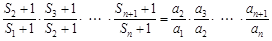 ,
,
化简,得 .① 4分
.① 4分
∴当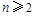 时,
时,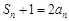 .②
.②
② -①,得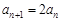 ,∴
,∴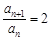 (
(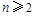 ). 6分
). 6分
∵当n = 1时, 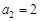 ,∴n = 1时上式也成立,
,∴n = 1时上式也成立,
∴数列{an}是首项为1,公比为2的等比数列, an = 2n-1(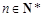 ). 8分
). 8分
(2)令n = 1,得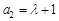 .令n = 2,得
.令n = 2,得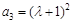 . 10分
. 10分
要使数列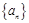 是等差数列,必须有
是等差数列,必须有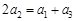 ,解得λ = 0. 11分
,解得λ = 0. 11分
当λ = 0时,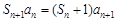 ,且
,且 .
.
当n≥2时,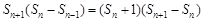 ,
,
整理,得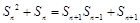 ,
,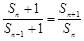 , 13分
, 13分
从而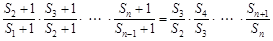 ,
,
化简,得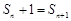 ,所以
,所以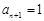 15分
15分
综上所述,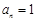 (
(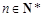 ),
),
所以λ = 0时,数列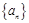 是等差数列. 16分
是等差数列. 16分
考点:已知 求
求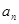

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前n项和为Sn,且满足
的前n项和为Sn,且满足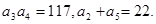
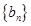 中的
中的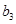 、
、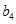 、
、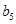 .
. ,求证:数列
,求证:数列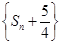 是等比数列.
是等比数列. 中,
中,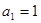 ,
,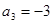 .
.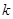 项和
项和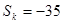 ,求
,求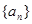 的公差不为零,其前n项和为
的公差不为零,其前n项和为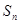 ,若
,若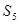 =70,且
=70,且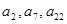 成等比数列,
成等比数列,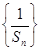 的前n项和为
的前n项和为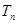 ,求证:
,求证: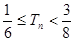 .
.