题目内容
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)![]() ;(2)第一种方案;(3)详见解析
;(2)第一种方案;(3)详见解析
【解析】
(1)计算出从![]() 个水果中随机抽取一个,抽到礼品果的概率;则可利用二项分布的概率公式求得所求概率;(2)计算出方案
个水果中随机抽取一个,抽到礼品果的概率;则可利用二项分布的概率公式求得所求概率;(2)计算出方案![]() 单价的数学期望,与方案
单价的数学期望,与方案![]() 的单价比较,选择单价较低的方案;(3)根据分层抽样原则确定抽取的
的单价比较,选择单价较低的方案;(3)根据分层抽样原则确定抽取的![]() 个水果中,精品果
个水果中,精品果![]() 个,非精品果
个,非精品果![]() 个;则
个;则![]() 服从超几何分布,利用超几何分布的概率计算公式可得到每个
服从超几何分布,利用超几何分布的概率计算公式可得到每个![]() 取值对应的概率,从而可得分布列;再利用数学期望的计算公式求得结果.
取值对应的概率,从而可得分布列;再利用数学期望的计算公式求得结果.
(1)设从![]() 个水果中随机抽取一个,抽到礼品果的事件为
个水果中随机抽取一个,抽到礼品果的事件为![]() ,则
,则![]()
现有放回地随机抽取![]() 个,设抽到礼品果的个数为
个,设抽到礼品果的个数为![]() ,则
,则![]()
![]() 恰好抽到
恰好抽到![]() 个礼品果的概率为:
个礼品果的概率为:![]()
(2)设方案![]() 的单价为
的单价为![]() ,则单价的期望值为:
,则单价的期望值为:
![]()
![]()
![]() 从采购商的角度考虑,应该采用第一种方案
从采购商的角度考虑,应该采用第一种方案
(3)用分层抽样的方法从![]() 个水果中抽取
个水果中抽取![]() 个,则其中精品果
个,则其中精品果![]() 个,非精品果
个,非精品果![]() 个
个
现从中抽取![]() 个,则精品果的数量
个,则精品果的数量![]() 服从超几何分布,所有可能的取值为:
服从超几何分布,所有可能的取值为:![]()
则![]() ;
;![]() ;
;![]() ;
;![]()
![]() 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
|
|
![]()

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 50 | 200 | 350 | 300 | 100 |
乙电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 250 | 300 | 150 | 100 | 200 |
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
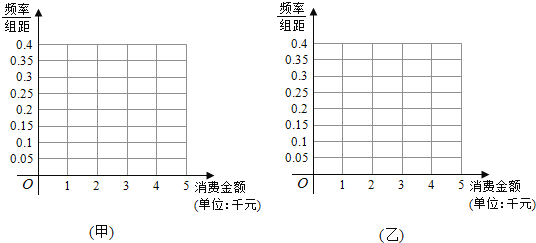
(Ⅱ)(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.