题目内容
【题目】已知椭圆![]()
![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 经过椭圆C的上、下顶点.
经过椭圆C的上、下顶点.
(1)求椭圆C的方程;
(2)若直线l与椭圆C相切,且与椭圆![]() 相交于M,N两点,证明:
相交于M,N两点,证明:![]() 的面积为定值(O为坐标原点).
的面积为定值(O为坐标原点).
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据圆![]() 经过椭圆C的上、下顶点,可得
经过椭圆C的上、下顶点,可得![]() ,再根据离心率即可求得椭圆方程.
,再根据离心率即可求得椭圆方程.
(2)分斜率存在与否两种情况讨论,分别计算出![]() 的面积,即可得证.
的面积,即可得证.
(1)解:因为圆![]() 过椭圆C的上、下顶点,所以
过椭圆C的上、下顶点,所以![]() .
.
又离心率![]() ,所以
,所以![]() ,则
,则![]() .
.
故椭圆C的方程为![]() .
.
(2)证明:椭圆![]() ,
,
当直线l的斜率不存在时,这时直线l的方程为![]() ,
,
联立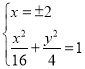 ,得
,得![]() ,即
,即![]() ,
,
则![]() .
.
当直线l的斜率存在时,设![]() ,
,
联立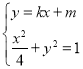 ,得
,得![]() ,
,
由![]() ,可得
,可得![]() .
.
联立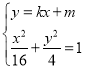 ,得
,得![]() .
.
设![]()
![]() ,所以
,所以![]()
![]() ,
,
则
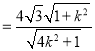 .
.
因为原点到直线l的距离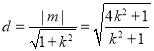 ,
,
所以![]() .
.
综上所述,![]() 的面积为定值
的面积为定值![]() .
.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
x(单位:元) | 30 | 40 | 50 | 60 |
y(单位:万人) | 4.5 | 4 | 3 | 2.5 |
(1)若y与x具有较强的相关关系,试分析y与x之间是正相关还是负相关;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)根据(2)中求出的线性回归方程,预测票价定为多少元时,能获得最大票房收入.
参考公式: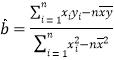 ,
,![]() .
.
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.某机构组织了一场诗词知识竞赛,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,从中随机抽取100名选手进行调查,如图是根据调查结果绘制的选手等级与人数的条形图.
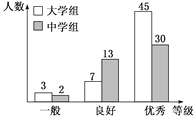
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此判断能否在犯错误的概率不超过0.05的前提下认为选手成绩优秀与文化程度有关?
优秀 | 合格 | 总计 | |
大学组 | |||
中学组 | |||
总计 |
(2)若参赛选手共6万名,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中选取6名,在良好等级的选手中选取6名,都依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为a,在选出的6名良好等级的选手中任取一名,记其编号为b,求使得方程组![]() 有唯一一组实数解(x,y)的概率.
有唯一一组实数解(x,y)的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |