题目内容
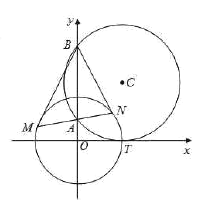
【题目】如图,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴交于两点
轴正半轴交于两点![]() ,
,![]() (
(![]() 在
在![]() 的上方),且
的上方),且![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作任一条直线与圆
作任一条直线与圆![]() :
:![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
①求证:![]() 为定值,并求出这个定值;
为定值,并求出这个定值;
②求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() (2)①
(2)①![]() ;证明见解析②
;证明见解析②![]()
【解析】
(1)由直线与圆相交,利用勾股定理构建方程求得半径,得答案;
(2)①分类讨论![]() 是否存在,当
是否存在,当![]() 存在时,可联立直线与圆的方程,进而确定
存在时,可联立直线与圆的方程,进而确定![]() 的关系,利用斜率k分别表示
的关系,利用斜率k分别表示![]() ,
,![]() ,再利用弦长公式表示
,再利用弦长公式表示![]() ,作商并化简,得答案;当
,作商并化简,得答案;当![]() 不存在时,M为特殊位置,直接表示
不存在时,M为特殊位置,直接表示![]() ,作商,得答案;
,作商,得答案;
②利用点到直线的距离公式表示点B到![]() 的距离,利用弦长公式表示
的距离,利用弦长公式表示![]() ,最后表示所求
,最后表示所求![]() 的面积,借助换元法求得函数的最大值即可.
的面积,借助换元法求得函数的最大值即可.
(1)由题可知点![]() ,所以可以设圆心
,所以可以设圆心![]()
因为![]() ,所以由
,所以由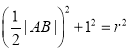 ,解得
,解得![]() ,所以
,所以![]()
所以圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)①证明:由(1)可得![]() ,
,![]()
当![]() 存在时,设
存在时,设![]()
将直线和圆的方程联立: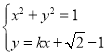
得![]() ——Ⅰ
——Ⅰ
设![]() ,
,![]() ,且
,且![]() ,
,
那么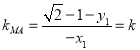 ,
,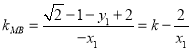
所以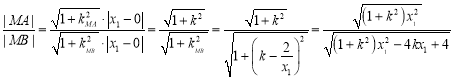 ——Ⅱ
——Ⅱ
由Ⅰ得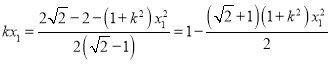 ,
,
将其代入Ⅱ化简可得![]() ;
;
当![]() 不存在时,显然
不存在时,显然![]() 为
为![]() 或
或![]()
此时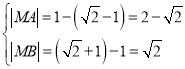 或
或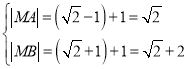
则![]()
综上所述:![]() 为定值
为定值![]()
②由题可知此时![]() 必然存在,仍设
必然存在,仍设![]()
则点B到![]() 的距离为:
的距离为: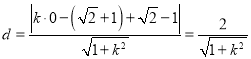
由①可知Ⅰ式:![]()
则![]()
所以![]()
故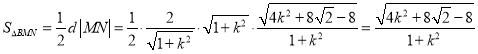
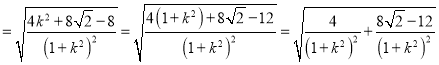
令![]() ,则
,则![]()
其内部函数开口向上,对称轴为
故当![]() 时,
时,![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目