题目内容
【题目】已知一次函数
是
上的减函数，
,且 f [ f(x)]=16x-3.
（1）求；
（2）若
在(-2,3)单调递增，求实数
的取值范围；
（3）当
时，有最大值1，求实数的值.
【答案】（1）
； （2）
； （3）
.
【解析】
⑴设
，结合题意运用待定系数法求出表达式
⑵表示出
的解析式，结合单调性求出
的取值范围
⑶讨论对称轴与区间的位置关系，求出实数的值
（1）∵
是
上的增函数，
设f(x)=ax+b(a<0)
故f[f(x)]=a(ax+b)+b=a2x+ab+b=16x-3,
∴a=16,ab+b=-5,解得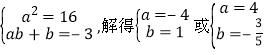
由于a<0,得a=-4,b=1 ,∴f(x)=-4x+1.
（2）
=(-4x+1)(x+m)=-4x2+(1-4m)x+m
对称轴
，根据题意可得
3， 解得
,
∴的取值范围为
。
（3）①当 
即
时,
，解得m=
，符合题意；
②当>1时，即
时,
=1,解得m=
,
不符合题意；
由①②可得m=.
练习册系列答案
相关题目
【题目】探究函数
，x∈(0，+∞)取最小值时x的值，列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题:
(1)函数(x>0)在区间(0，2)上递减；函数
在区间________上递增.当x=_________时，
_______.
(2)证明:函数(x>0)在区间(O，2)上递减.
