题目内容

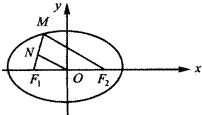
如图，椭圆
x2
25
+
y2
9
=1上的点M到焦点F1的距离为2，N为MF1的中点，则|ON|（O为坐标原点）的值为（　　）
A．4B．2C．8D．
3
2

∵椭圆方程为
x2
25
+
y2
9
=1，
∴椭圆的a=5，长轴2a=10，可得椭圆上任意一点到两个焦点F1、F2距离之和等于10．
∴|MF1|+|MF2|=10
∵点M到左焦点F1的距离为2，即|MF1|=2，
∴|MF2|=10-2=8，
∵△MF1F2中，N、O分别是MF1、F1F2中点
∴|ON|=
1
2
|MF2|=4．
故选A．
练习册系列答案
相关题目
椭圆
x2
36
+
y2
20
=1的离心率e是（　　）
A．
5
3
B．
3
2
C．
3
5
5
D．
2
3
曲线
x2
36
+
y2
9
=1与曲线
x2
36-k
+
y2
9-k
=1(k＜9)的（　　）
A．长、短轴相等B．准线相等
C．离心率相等D．焦距相等
已知椭圆
x2
16
+
y2
9
=1的左、右焦点分别为F1、F2，P是椭圆上的一点，Q是PF1的中点，若|OQ|=1，则|PF1|=______．
已知P为椭圆
x2
16
+
y2
12
=1上动点，F为椭圆的右焦点，点A的坐标为（3，1），则|PA|+2|PF|的最小值为（　　）
A．10+
2
B．10-
2
C．5D．7
椭圆x2+
y2
4
=1的焦点到直线
2
x-y=0的距离为（　　）
A．
2
B．
3
C．1D．
2
2
如图，F1、F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2=60°．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）已知△AF1B的面积为40
3
，求a，b的值．
已知椭圆
x2
20
+
y2
k
=1的焦距为6，则k的值为（　　）
A．13或27B．11或29C．15或28D．10或26
曲线
x2
16
+
y2
9
=1的长轴长为（　　）
A．8B．4C．6D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网