题目内容

已知P为椭圆
x2
16
+
y2
12
=1上动点，F为椭圆的右焦点，点A的坐标为（3，1），则|PA|+2|PF|的最小值为（　　）
A．10+
2
B．10-
2
C．5D．7
∵椭圆
x2
16
+
y2
12
=1的a=4，b=2
3
，c=2
e=
1
2
，
∴|PA|+2|PF|即为：|PA|+
1
e
|PF|
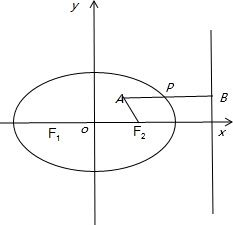
∴根据椭圆的第二定义：
过A作右准线的垂线，交与B点，
则|PA|+
1
e
|PF|的最小值为|AB|
∵|AB|=5
∴|PA|+
1
e
|PF|的最小值为：5
故答案为：5．
练习册系列答案
相关题目
已知集合A={x|-2≤x≤10，x∈Z}，m，n∈A，方程
x2
m
+
y2
n
=1表示焦点在x轴上的椭圆，则这样的椭圆共有______个．
已知椭圆C短轴的一个端点为（0，1），离心率为
2
2
3
．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设直线y=x+m交椭圆C于A、B两点，若|AB|=
6
3
5
，求m．
如图点F是椭圆的焦点，P是椭圆上一点，A，B是椭圆的顶点，且PF⊥x轴，OP∥AB，那么该椭圆的离心率是（　　）
A．
2
4
B．
1
2
C．
2
2
D．
3
2
如下图，椭圆中心为O，F是焦点，A为顶点，准线l交OA延长线于B，P，Q在椭圆上且PD⊥l于D，QF⊥OA于F，则以下比值①
|PF|
|PD|
②
|QF|
|BF|
③
|AO|
|BO|
④
|AF|
|BA|
⑤
|FO|
|AO|
能作为椭圆的离心率的是______（填写所有正确的序号）
如图，椭圆
x2
25
+
y2
9
=1上的点M到焦点F1的距离为2，N为MF1的中点，则|ON|（O为坐标原点）的值为（　　）
A．4B．2C．8D．
3
2
椭圆
x2
4
+
y2
3
=1内有一点P（1，-1），F为椭圆的右焦点，在椭圆上有一动点M，则|MP|+|MF|的取值范围为______．
已知F是椭圆5x2+9y2=45的右焦点，P为该椭圆上的动点，A（2，1）是一定点．
（1）求|PA|+
3
2
|PF|的最小值，并求相应点P的坐标；
（2）求|PA|+|PF|的最大值与最小值；
（3）过点F作倾斜角为60°的直线交椭圆于M、N两点，求|MN|；
（4）求过点A且以A为中点的弦所在的直线方程．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的长、短轴端点分别为A、B，从椭圆上一点M（在x轴上方）向x轴作垂线，恰好通过椭圆的左焦点F1，
AB
∥
OM
．
（1）求椭圆的离心率e；
（2）设Q是椭圆上任意一点，F1、F2分别是左、右焦点，求∠F1QF2的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网