题目内容
13.在2013年春节期间,某市物价部门,对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如下表所示:| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
(1)求销售量y对商品的价格x的回归直线方程;
(2)欲使销售量为12,则价格应定为多少.
附:在回归直线$y=\hat bx+\hat a$中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
分析 (1)首先做出两组数据的平均数,利用最小二乘法得到线性回归方程的系数,写出线性回归方程;
(2)令y=-3.2x+40=12,可预测销售量为12件时的售价.
解答 解:(1)由题意知$\overline{x}$=10,$\overline{y}$=8,
∴b=$\frac{99+95+80+63+11-5×10×8}{81+90.25+100+110.25+121-5×100}$=-3.2,a=8-(-3.2)×10=40,
∴线性回归方程是y=-3.2x+40;
(2)令y=-3.2x+40=12,可得x=8.75,
∴预测销售量为12件时的售价是8.75元.
点评 本题考查求线性回归方程,考查学生的计算能力,是一个基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知方程ex-x+a=0(a为常数)有两个不等实根,则实数a的取值范围是( )
| A. | (0,1) | B. | (-1,0) | C. | (-∞,-1) | D. | (-∞,-1] |
5.设一个线性回归方程y=3-2x,变量x增加一个单位时( )
| A. | y平均增加2个单位 | B. | y平均减少3个单位 | ||
| C. | y平均减少2个单位 | D. | y平均增加3个单位 |
 如图,E为矩形ABCD所在平面外一点,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
如图,E为矩形ABCD所在平面外一点,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
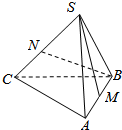 如图,正四面体S-ABC中,其棱长为2.
如图,正四面体S-ABC中,其棱长为2.