题目内容
8. 如图,E为矩形ABCD所在平面外一点,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,
如图,E为矩形ABCD所在平面外一点,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)G为矩形ABCD对角线的交点,求三棱锥C-BGF的体积.
分析 (Ⅰ)先证明AE⊥BC,再证AE⊥BF,由线面垂直的判定定理证明结论.
(Ⅱ)运用等体积法,先证FG⊥平面BCF,把原来的三棱锥的底换成面BCF,则高就是FG,代入体积公式求三棱锥的体积.
解答 (Ⅰ)证明:∵AD⊥平面ABE,AD∥BC,
∴BC⊥平面ABE,则AE⊥BC.又∵BF⊥平面ACE,则AE⊥BF
∴AE⊥平面BCE.
(Ⅱ)解:∵AE∥平面BFD,∴AE∥FG,而AE⊥平面BCE,
∴FG⊥平面BCE,∴FG⊥平面BCF,
∵G是AC中点,∴F是CE中点,且FG=$\frac{1}{2}$AE=1,
∵BF⊥平面ACE,∴BF⊥CE.
∴Rt△BCE中,BF=CF=$\frac{1}{2}$CE=$\sqrt{2}$.
∴S△CFB=$\frac{1}{2}•\sqrt{2}•\sqrt{2}$=1
∴VC-BFG=VG-BCF=$\frac{1}{3}$S△CFB•FG=$\frac{1}{3}$.
点评 本题考查线面垂直的证明方法,利用等体积法求三棱锥的体积,属于中档题.

练习册系列答案
相关题目
13.在2013年春节期间,某市物价部门,对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如下表所示:
通过分析,发现销售量y对商品的价格x具有线性相关关系.
(1)求销售量y对商品的价格x的回归直线方程;
(2)欲使销售量为12,则价格应定为多少.
附:在回归直线$y=\hat bx+\hat a$中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
(1)求销售量y对商品的价格x的回归直线方程;
(2)欲使销售量为12,则价格应定为多少.
附:在回归直线$y=\hat bx+\hat a$中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
18.如果袋中有六个红球,四个白球,从中任取一球,确认颜色后放回,重复摸取四次,设X为取得红球的次数,那么X的均值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{12}{5}$ | C. | $\frac{19}{7}$ | D. | $\frac{1}{3}$ |
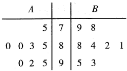 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.