题目内容
3. 如图,正四面体S-ABC中,其棱长为2.
如图,正四面体S-ABC中,其棱长为2.(1)求该几何体的体积;
(2)已知M,N分别是棱AB和SC的中点.求直线BN和直线SM所成的角的余弦值.
分析 (1)取三角形ABC 的中心O,连接SO,说明SO为正四面体的高,求出底面面积与高,即可求解几何体的体积.
(2)连接MC,取MC中点E,连接BE,NE,BN,说明直线BN和直线NE所成的角即为直线BN和直线SM所成的角.通过解三角形求解即可.
解答 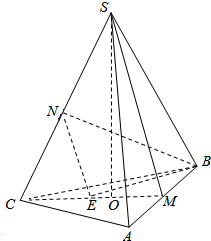 解:(1)取三角形ABC 的中心O,连接SO,
解:(1)取三角形ABC 的中心O,连接SO,
由正四面体的性质知$SO=\sqrt{S{M^2}-O{M^2}}=\frac{{2\sqrt{6}}}{3}$,
SO为正四面体的高,$\begin{array}{c}{S}_{△ABC}=\sqrt{3}\end{array}\right.$,
$V=\frac{1}{3}{S}_{△ABC}•SO=\frac{2\sqrt{2}}{3}$…(6分)
(2)连接MC,取MC中点E,连接BE,NE,BN,则NE平行于SB.
则直线BN和直线NE所成的角即为直线BN和直线SM所成的角.
BN=$\sqrt{3}$,NE=$\frac{{\sqrt{3}}}{2}$,BE=$\sqrt{E{M^2}+M{B^2}}=\frac{{\sqrt{7}}}{2}$,
∴$\begin{array}{l}cos∠BNE=\frac{{B{N^2}+N{E^2}-B{E^2}}}{2BN•NE}=\frac{2}{3}\end{array}$,
∴该几何体的体积$\frac{2\sqrt{2}}{3}$,
直线BN和直线SM所成的角的余弦值$\frac{2}{3}$.…(12分).
点评 本题考查几何体的体积的求法,异面直线所成角的求法,考查计算能力以及空间想象能力逻辑推理能力..

练习册系列答案
相关题目
13.在2013年春节期间,某市物价部门,对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如下表所示:
通过分析,发现销售量y对商品的价格x具有线性相关关系.
(1)求销售量y对商品的价格x的回归直线方程;
(2)欲使销售量为12,则价格应定为多少.
附:在回归直线$y=\hat bx+\hat a$中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
(1)求销售量y对商品的价格x的回归直线方程;
(2)欲使销售量为12,则价格应定为多少.
附:在回归直线$y=\hat bx+\hat a$中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
18.如果袋中有六个红球,四个白球,从中任取一球,确认颜色后放回,重复摸取四次,设X为取得红球的次数,那么X的均值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{12}{5}$ | C. | $\frac{19}{7}$ | D. | $\frac{1}{3}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是梯形,DC∥AB,DC=2AB,O为AC与BD的交点,E是棱PA上一点,且OE∥平面PBC,求$\frac{AE}{PE}$的值.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,DC∥AB,DC=2AB,O为AC与BD的交点,E是棱PA上一点,且OE∥平面PBC,求$\frac{AE}{PE}$的值.