题目内容
【题目】已知
的展开式中第五项的系数与第三项的系数的比是10∶1.
(1)求展开式中各项系数的和；
(2)求展开式中含
的项；
(3)求展开式中系数最大的项和二项式系数最大的项．
【答案】(1)1；(2)－16
.(3)答案见解析.
【解析】试题分析：
(1)利用赋值法，令
可得展开式中各项系数的和是1.
(2)首先写出通项公式，据此可得展开式中含
的项是－16
.
(3)由题意求解不等式即可求得系数最大的项和二项式系数最大的项分别为T7＝1 792
和T5＝1 120
.
试题解析：
由题意知，第五项系数为
，第三项的系数为
，则有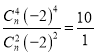
，化简得n2－5n－24＝0，解得n＝8或n＝－3(舍去)．
(1)令x＝1得各项系数的和为(1－2)8＝1.
(2)通项公式
＝
＝
，
令
－2k＝
，则k＝1，故展开式中含
的项为T2＝－16
.
(3)设展开式中的第k项，第k＋1项，第k＋2项的系数绝对值分别为
， 
， 
，
若第k＋1项的系数绝对值最大，则
解得5
.
又T6的系数为负，∴系数最大的项为T7＝1 792
.
由n＝8知第5项二项式系数最大，此时T5＝1 120
.
练习册系列答案
相关题目
【题目】某校举行汉字听写比赛，为了了解本次比赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数，满分100分)进行统计，请根据频率分布表中所提供的数据，解答下列问题：
组号 | 分组 | 频数 | 频率 |
第1组 | [50，60) | 5 | 0.05 |
第2组 | [60，70) |
| 0.35 |
第3组 | [70，80) | 30 |
|
第4组 | [80，90) | 20 | 0.20 |
第5组 | [90，100] | 10 | 0.10 |
合计 | 100 | 1.00 |
（Ⅰ）求
的值；
（Ⅱ）若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛，并从中选出2人做种子选手，求2人中至少有1人是第4组的概率。
