题目内容
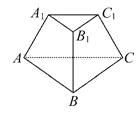
【题目】如图，△ABC与△A1B1C1不全等，且A1B1∥AB，B1C1∥BC，C1A1∥CA.求证：AA1，BB1，CC1交于一点.
【答案】见解析
【解析】试题分析：先根据条件确定两直线相交，设交于一点，再利用两平面的公共点必在这两平面交线上证交点在第三条直线上
试题解析：如图所示，因为A1B1∥AB，
所以A1B1与AB确定一平面，记为平面α.
同理，将B1C1与BC所确定的平面记为平面β，C1A1与CA所确定的平面记为平面γ.
易知β∩γ=C1C.
又△ABC与△A1B1C1不全等，
所以AA1与BB1相交，设交点为P，P∈AA1，P∈BB1.
而AA1γ，BB1β，所以P∈γ，P∈β，
所以P在平面β与平面γ的交线上.
又β∩γ=C1C，所以P∈C1C，
所以AA1，BB1，CC1交于一点.
练习册系列答案
相关题目
【题目】某项科研活动共进行了5次试验，其数据如下表所示：
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
（1）从5次特征量
的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；
（2）求特征量
关于
的线性回归方程
；并预测当特征量
为570时特征量
的值.
（附：回归直线的斜率和截距的最小二乘法估计公式分别为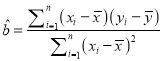
， 
）
