题目内容
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
【答案】(1) 35,0.30;(2) ![]() .
.
【解析】试题分析:(Ⅰ)直接利用频率和等于1求出b,用样本容量乘以频率求a的值;
(Ⅱ)由分层抽样方法求出所抽取的6人中第三、第四、第五组的学生数,利用列举法写出从中任意抽取2人的所有方法种数,查出2人至少1人来自第四组的事件个数,然后利用古典概型的概率计算公式求解.
试题解析:
(Ⅰ)a=100-5-30-20-10=35,b=1-0.05-0.35-0.20-0.10=0.30
(Ⅱ )因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,
每组分别为,第3组: ![]() ×30=3人,第4组:
×30=3人,第4组: ![]() ×20=2人,第5组:
×20=2人,第5组: ![]() ×10=1人,
×10=1人,
所以第3、4、5组应分别抽取3人、2人、1人
设第3组的3位同学为A1、A2、A3,第4组的2位同学为B1、B2,第5组的1位同学为C1,则从6位同学中抽2位同学有15种可能,如下:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1).其中第4组被入选的有9种,
所以其中第4组的2位同学至少有1位同学入选的概率为![]() =
=![]()

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为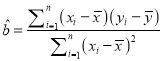 ,
, ![]() )
)
