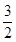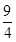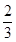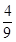题目内容
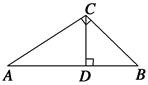
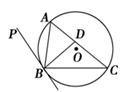
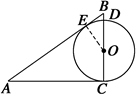
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,以BC上一点O为圆心作⊙O与AB相切于E,与AC相切于C,又⊙O与BC的另一个交点为D,则线段BD的长为
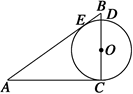

| A.1 | B.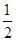 | C.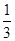 | D.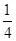 |
C
⊙O与AC相切于C,则∠ACB=90°,又AC=4,BC=3,∴AB=5,连接OE,且设⊙O的半径为R,则由△OEB∽△ACB,
∴OB= =
= R,
R,
∴BC=OC+OB=R+ R=
R=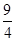 R=3,
R=3,
∴R=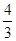 ,∴BD=BC-2R=3-
,∴BD=BC-2R=3-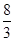 =
=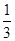 .
.

∴OB=
 =
= R,
R,∴BC=OC+OB=R+
 R=
R=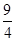 R=3,
R=3,∴R=
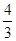 ,∴BD=BC-2R=3-
,∴BD=BC-2R=3-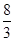 =
=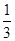 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
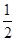 ,∠D=30°.
,∠D=30°.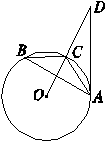
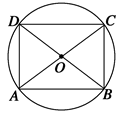
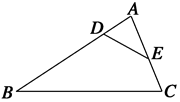
 =
=
 =
=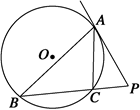

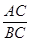 的值为
的值为