题目内容
如图,三棱锥 中,
中, 底面
底面 ,
, ,
,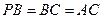 ,点
,点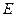 、
、 分别是
分别是 、
、 的中点.
的中点.

(1)求证: ⊥平面
⊥平面 ;(2)求二面角
;(2)求二面角 的余弦值。
的余弦值。
 中,
中, 底面
底面 ,
, ,
,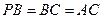 ,点
,点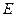 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:
 ⊥平面
⊥平面 ;(2)求二面角
;(2)求二面角 的余弦值。
的余弦值。(Ⅰ) 略 (Ⅱ) 

:方法(一)
(Ⅰ)由已知可得 为等腰直角三角形,则
为等腰直角三角形,则 .
.
由 平面
平面 ,
, 平面
平面 ,则
,则 .
.
又 ,
, ,
,
则 平面
平面 ,由
,由 平面
平面 ,得
,得 .
.
由中位线定理得, ,于是
,于是 ,
,
又 ,所以
,所以 平面
平面 .
.
(Ⅱ)已证明 平面
平面 ,又
,又 平面
平面 ,则
,则 .
.
已证明 ,又
,又 ,则
,则 平面
平面 .
.
因为 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
, .
.
由二面角的定义,得 为二面角
为二面角 的平面角.
的平面角.
设 ,可求得
,可求得 ,
, ,
,
在 中,可求得
中,可求得 ,在
,在 中,可求得
中,可求得 ,
,
在 中,由余弦定理得,
中,由余弦定理得, .则
.则 为所求.
为所求.
方法(二)如图建立空间直角坐标系,设 ,
,
可求出以下各点的坐标:
A(2,2,0),B(0,0,0),C(2,0,0),
P(0,0,2),E(1,0,1),F(1,1,1)
(Ⅰ) ,
, ,
,
有 ,
, ,
,
于是 ,
, ,又
,又 ,
,
则 平面
平面 .
.
(Ⅱ) ,有
,有 ,
, ,
,
于是 ,
, ,由二面角定义,向量
,由二面角定义,向量 与
与 的夹角为所求.
的夹角为所求.
 ,所以
,所以 为所求.
为所求.
(Ⅰ)由已知可得
 为等腰直角三角形,则
为等腰直角三角形,则 .
.由
 平面
平面 ,
, 平面
平面 ,则
,则 .
.又
 ,
, ,
,则
 平面
平面 ,由
,由 平面
平面 ,得
,得 .
.由中位线定理得,
 ,于是
,于是 ,
,又
 ,所以
,所以 平面
平面 .
. (Ⅱ)已证明
 平面
平面 ,又
,又 平面
平面 ,则
,则 .
.已证明
 ,又
,又 ,则
,则 平面
平面 .
.因为
 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
, .
.由二面角的定义,得
 为二面角
为二面角 的平面角.
的平面角.设
 ,可求得
,可求得 ,
, ,
,在
 中,可求得
中,可求得 ,在
,在 中,可求得
中,可求得 ,
,在
 中,由余弦定理得,
中,由余弦定理得, .则
.则 为所求.
为所求.
|
 ,
,可求出以下各点的坐标:
A(2,2,0),B(0,0,0),C(2,0,0),
P(0,0,2),E(1,0,1),F(1,1,1)
(Ⅰ)
 ,
, ,
,
有
 ,
, ,
,于是
 ,
, ,又
,又 ,
,则
 平面
平面 .
. (Ⅱ)
 ,有
,有 ,
, ,
,于是
 ,
, ,由二面角定义,向量
,由二面角定义,向量 与
与 的夹角为所求.
的夹角为所求. ,所以
,所以 为所求.
为所求.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

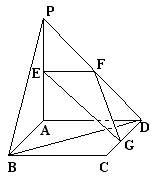
 的一条斜线,点A是平面
的一条斜线,点A是平面 是经过点A的一条动直线,那么下列情形中可能出现的是 ( )
是经过点A的一条动直线,那么下列情形中可能出现的是 ( )



 a.
a.




 ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
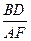 为何值时,平面DEF
为何值时,平面DEF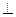 平面BEF?并证明你的结论。(8分)
平面BEF?并证明你的结论。(8分)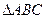 中,
中,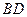 为
为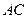 边上高,
边上高,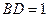 ,
,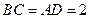 ,沿
,沿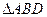 翻折,使得
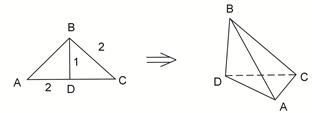
翻折,使得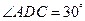 ,得到几何体
,得到几何体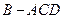 。(1)求证:
。(1)求证: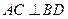 ;
;
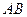 与平面
与平面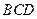 成角的正切值。
成角的正切值。