题目内容
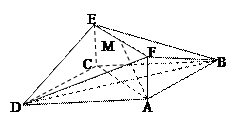
如图,菱形ABCD所在平面与矩形ACEF所在平面相互垂直,点M是线段EF的中点。(1)求证:AM // 平面BDE(6分) (2)当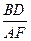 为何值时,平面DEF
为何值时,平面DEF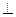 平面BEF?并证明你的结论。(8分)
平面BEF?并证明你的结论。(8分)
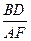 为何值时,平面DEF
为何值时,平面DEF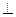 平面BEF?并证明你的结论。(8分)
平面BEF?并证明你的结论。(8分)(Ⅰ)略 (Ⅱ) 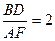 …
…
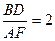 …
…
证明(1)取AC与BD的交点N,连接EN, 1分
由题意知:EN // AM, 4分又EN在平面BDE内, …5分
所以AM // 平面BDE ……6分
(2)当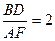 时,平面DEF
时,平面DEF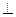 平面BEF……7分
平面BEF……7分
因为面ACEF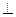 面ABCD,四边形ACEF为矩形,
面ABCD,四边形ACEF为矩形,
所以FA、EC都垂直于面ABCD,又四边形ABCD是菱形,
所以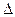 FAD
FAD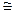
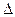 ECA,所以DF=DE又M为EF的中点,所以DM
ECA,所以DF=DE又M为EF的中点,所以DM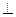 EF,………10分
EF,………10分
当DM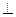 BM时,就有DM
BM时,就有DM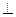 平面BEF …12分
平面BEF …12分
即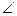 DMB=90
DMB=90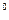 时,平面DEF
时,平面DEF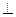 平面BEF ∴
平面BEF ∴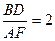 ……14分
……14分
由题意知:EN // AM, 4分又EN在平面BDE内, …5分
所以AM // 平面BDE ……6分
(2)当
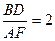 时,平面DEF
时,平面DEF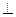 平面BEF……7分
平面BEF……7分因为面ACEF
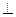 面ABCD,四边形ACEF为矩形,
面ABCD,四边形ACEF为矩形,所以FA、EC都垂直于面ABCD,又四边形ABCD是菱形,
所以
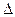 FAD
FAD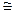
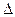 ECA,所以DF=DE又M为EF的中点,所以DM
ECA,所以DF=DE又M为EF的中点,所以DM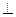 EF,………10分
EF,………10分当DM
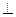 BM时,就有DM
BM时,就有DM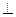 平面BEF …12分
平面BEF …12分即
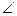 DMB=90
DMB=90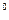 时,平面DEF
时,平面DEF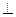 平面BEF ∴
平面BEF ∴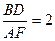 ……14分
……14分
练习册系列答案
相关题目
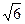 ,A是线段PD的中点,E是线段AB的中点;如图⑵,沿AB把平面PAB折起,使二面角P-CD-B成45
,A是线段PD的中点,E是线段AB的中点;如图⑵,沿AB把平面PAB折起,使二面角P-CD-B成45 角.
角.
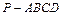 中,
中,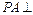 底面
底面 ,
,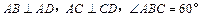 ,
,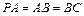 ,
, 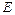 是
是 的中点.
的中点.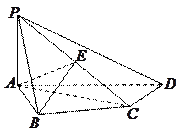 (1)证明
(1)证明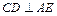 ;
;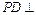 平面
平面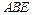 ;
;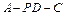 的大小.
的大小.
 中,
中, 底面
底面 ,
, ,
,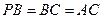 ,点
,点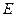 、
、 分别是
分别是 、
、 的中点.
的中点.
 ;(2)求二面角
;(2)求二面角 的余弦值。
的余弦值。 AED沿AE折起到
AED沿AE折起到 的位
的位 置时,有平面
置时,有平面
 平面ABCE,
平面ABCE,
 (如图)
(如图) 求点D/到平面ABCE的距离.
求点D/到平面ABCE的距离. 中,截面
中,截面 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )

 ∥截面
∥截面
 与
与 所成的角为
所成的角为
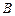 为等腰直角
为等腰直角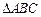 的直角顶点,
的直角顶点,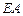 、
、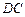 都垂直于
都垂直于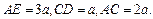

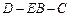 的大小;
的大小;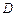 到平面
到平面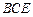 的距离;
的距离;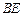 上是否存在一点
上是否存在一点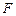 ,使得
,使得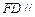 平面
平面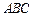 且
且 若存在,请指出
若存在,请指出