题目内容
4.已知函数$f(x)=\left\{{\begin{array}{l}{{{log}_{\frac{1}{3}}}x,}&{x>0}\\{{2^x},}&{x≤0}\end{array}}\right.$,则f(f(9))=$\frac{1}{4}$,若f(a)>$\frac{1}{2}$,则实数a的取值范围是(-1,$\frac{\sqrt{3}}{3}$).分析 利用分段函数求法第一问,通过分类讨论求解指数与对数不等式解答第二问.
解答 解:函数$f(x)=\left\{{\begin{array}{l}{{{log}_{\frac{1}{3}}}x,}&{x>0}\\{{2^x},}&{x≤0}\end{array}}\right.$,则f(f(9))=f(-2)=2-2=$\frac{1}{4}$.
当a>0时,${log}_{\frac{1}{3}}a>\frac{1}{2}$,可得:a<$\frac{\sqrt{3}}{3}$.
当a≤0时,${2}^{a}>\frac{1}{2}$,解得a>-1,
综上a∈(-1,$\frac{\sqrt{3}}{3}$).
故答案为:$\frac{1}{4}$;(-1,$\frac{\sqrt{3}}{3}$).
点评 本题考查分段函数的应用,函数值的求法,指数以及对数不等式的解法,考查计算能力.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
14.某农民在一块耕地上种植一种作物,每年种植成本为800元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
(Ⅰ)设X表示该农民在这块地上种植1年此作物的利润,求X的分布列;
(Ⅱ)若在这块地上连续3年种植此作物,求这3年中第二年的利润少于第一年的概率.
| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.6 | 0.4 |
(Ⅱ)若在这块地上连续3年种植此作物,求这3年中第二年的利润少于第一年的概率.
12.某次数学测试后从两个班中各随机的抽取10名学生的数学成绩,作出它们的茎叶图如图所示,已知甲班的中位数为a1,标准差为s1,乙班的中位数为a2,标准差为s2,则由茎叶图可得( )
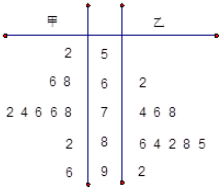

| A. | a1<a2,s1>s2 | B. | a1<a2,s1<s2 | C. | a1>a2,s1>s2 | D. | a1>a2,s1<s2 |