题目内容
【题目】已知等比数列{an}的前n项和为Sn,且满足Sn=2n+1+2p(n∈N*).
(1)求p的值及数列{an}的通项公式;
(2)若数列{bn}满足![]() =(3+p)anbn,求数列{bn}的前n项和Tn.
=(3+p)anbn,求数列{bn}的前n项和Tn.
【答案】(1)p=-1,an=2n(n∈N*).(2) ![]() .
.
【解析】试题分析:(1)根据和项与通项关系得当n≥2时,an=Sn-Sn-1=2n.根据n=1时也满足,得p的值及数列{an}的通项公式(2)由已知得bn=![]() ,再根据错位相减法求数列{bn}的前n项和Tn.
,再根据错位相减法求数列{bn}的前n项和Tn.
试题解析:(1)∵Sn=2n+1+2p(n∈N*),
∴a1=S1=4+2p,
当n≥2时,an=Sn-Sn-1=2n.
由于{an}是等比数列,
∴a1=4+2p=2,则p=-1,
因此an=2n(n∈N*).
(2)由![]() =(3+p)anbn=2anbn,得2n=22nbn,
=(3+p)anbn=2anbn,得2n=22nbn,
∴bn=![]() .
.
Tn=![]() +
+![]() +
+![]() +…+
+…+![]() ,①
,①
![]() Tn=
Tn=![]() +
+![]() +…+
+…+![]() +
+![]() ,②
,②
①-②得![]() Tn=
Tn=![]() +
+![]() +
+![]() +…+
+…+![]() -
-![]() ,
,
∴Tn=1+![]() +
+![]() +…+
+…+![]() -
-![]()
=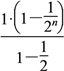 -
-![]() =2
=2![]() -
-![]() ,
,
因此Tn=2-![]() -
-![]() .
.

练习册系列答案
相关题目