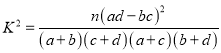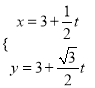题目内容
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,左,右焦点分别为F1,F2,上顶点和右顶点分别为B,A,线段AB的中点为D,且![]() ,△AOB的面积为
,△AOB的面积为![]() .
.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程.
,求以F2为圆心且与直线l相切的圆的方程.
【答案】(1)![]() ;(2)(x-2)2+y2=8.
;(2)(x-2)2+y2=8.
【解析】试题分析:(1)求椭圆方程关键是求方程![]() 中的
中的![]() ,题中有两个已知条件,由
,题中有两个已知条件,由![]() 用数学式子翻译出来联立方程组可解得;(2)先考虑当直线
用数学式子翻译出来联立方程组可解得;(2)先考虑当直线![]() 垂直于
垂直于![]() 轴时是否满足题意,如满足,求出相应圆方程,如不满足,则舍去,当直线
轴时是否满足题意,如满足,求出相应圆方程,如不满足,则舍去,当直线![]() 斜率存在时,可设方程为
斜率存在时,可设方程为![]() ,代入椭圆方程,由椭圆中的弦长公式求出弦长
,代入椭圆方程,由椭圆中的弦长公式求出弦长![]() ,再由点到直线距离公式求出
,再由点到直线距离公式求出![]() 到直线
到直线![]() 的距离,利用已知三角形面积求得
的距离,利用已知三角形面积求得![]() ,从而可得所求圆方程.
,从而可得所求圆方程.
试题解析:(1)设椭圆方程为![]() (a>b>0).由已知得A(a,0),B(0,b),D
(a>b>0).由已知得A(a,0),B(0,b),D![]() ,
,
所以kOD·kAB= ,
,
即a2=2b2,①
又S△AOB=![]() ,所以
,所以![]() ,②
,②
由①②解得a2=8,b2=4,
所以椭圆方程为![]() .
.
(2)①当直线l⊥x轴时,易得M(-2, ![]() ),N(-2,
),N(-2, ![]() ),△MF2N的面积为
),△MF2N的面积为![]() ,不合题意.
,不合题意.
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+2),代入椭圆方程得
(1+2k2)x2+8k2x+8k2-8=0.
显然有Δ>0,设M(x1,y1),N(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
所以MN=![]()
= ,
,
化简得MN=![]() .
.
又圆的半径![]() ,
,
所以![]() MN·r
MN·r
=![]() ×
×![]() ·
·![]()
=![]() ,
,
化简得k4+k2-2=0,解得k=±1,
所以r=![]() ,
,
所以所求圆的方程为(x-2)2+y2=8.

 阅读快车系列答案
阅读快车系列答案【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附: