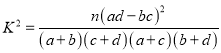题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() , 直线
, 直线![]() 过点
过点![]() .
.
(Ⅰ)若点![]() 到直线
到直线![]() 的距离为
的距离为![]() , 求直线
, 求直线![]() 的斜率;
的斜率;
(Ⅱ)设![]() 为抛物线上两点, 且
为抛物线上两点, 且![]() 不与
不与![]() 轴垂直, 若线段
轴垂直, 若线段![]() 的垂直平分线恰过点
的垂直平分线恰过点![]() , 求证: 线段
, 求证: 线段![]() 中点的横坐标为定值.
中点的横坐标为定值.
【答案】(Ⅰ) ![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(Ⅰ)设直线l的方程为y=k(x-4),由已知,抛物线C的焦点坐标为(1,0),因为点F到直线l的距离为![]() ,所以
,所以![]() ,由此能求出直线l的斜率;(Ⅱ)设线段AB中点的坐标为N
,由此能求出直线l的斜率;(Ⅱ)设线段AB中点的坐标为N![]() ,A
,A![]() ,B
,B![]() ,因为AB不垂直于x轴,所以直线MN的斜率为
,因为AB不垂直于x轴,所以直线MN的斜率为![]() ,直线AB的斜率为
,直线AB的斜率为![]() ,直线AB的方程为
,直线AB的方程为![]() ,由此能够证明线段AB中点的横坐标为定值
,由此能够证明线段AB中点的横坐标为定值
试题解析:(Ⅰ)由已知,x=4不合题意.设直线l的方程为y=k(x-4),
由已知,抛物线C的焦点坐标为(1,0),
因为点F到直线l的距离为![]() ,
,
所以![]() ,
,
解得![]() ,所以直线l的斜率为
,所以直线l的斜率为![]() .
.
(Ⅱ) 设线段![]() 中点的坐标为
中点的坐标为![]() ,
, ![]() ,
,
因为![]() 不垂直于
不垂直于![]() 轴,
轴,
则直线![]() 的斜率为
的斜率为![]() , 直线
, 直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
联立方程
消去![]() 得
得![]() ,
,
所以![]() ,
,
因为![]() 为
为![]() 中点, 所以
中点, 所以![]() , 即
, 即![]() ,
,
所以![]() .即线段
.即线段![]() 中点的横坐标为定值
中点的横坐标为定值![]() .
.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附: