题目内容
【题目】四棱锥A-BCDE中,侧棱AD⊥底面BCDE,底面BCDE是直角梯形,DE∥BC,BC⊥CD,BC=2AD=2DC=2DE=4,H,I分别是AD,AE的中点.

(Ⅰ)在AB上求作一点F,BC上求作一点G,使得平面FGI∥平面ACD;
(Ⅱ)求平面CHI将四棱锥A-BCDE分成的两部分的体积比.
【答案】(Ⅰ)见解析(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)通过证明 IG∥HC和FG∥AC.从而平面FGI∥平面ACD.
(Ⅱ)先求得四棱锥A-BCHI的体积V1=![]() ×
×![]() ×
×![]() =
=![]() ,和四棱锥A-BCDE的体积V=
,和四棱锥A-BCDE的体积V=![]() ×
×![]() ×(2+4)×2×2=4,通过作差得到多面体HI-ABCD的体积V2=V-V1=
×(2+4)×2×2=4,通过作差得到多面体HI-ABCD的体积V2=V-V1=![]() ,可得两部分体积比为
,可得两部分体积比为![]() .
.
试题解析:(Ⅰ)如右图所示,分别作AB的四等分点F(离A较近),BC的四等分点G(离C较近),则其使得平面FGI∥平面ACD.
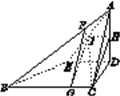
证明如下:
因为H,I分别是AD,AE的中点,
所以HI∥DE,
且HI=![]() DE.
DE.
又DE∥BC,BC=2DE,
所以HI∥BC且HI=![]() BC.
BC.
所以HI∥GC且HI=GC.
所以四边形HIGC是平行四边形.
所以IG∥HC.
由题意, ![]() ,所以FG∥AC.
,所以FG∥AC.
又IG∩FG=G,HC∩AC=C,所以平面FGI∥平面ACD.
(Ⅱ)连接BI,∵H,I分别为AD,AE中点,∴HI∥DE,HI=![]() DE=1,
DE=1,

又DE∥BC,∴HI∥BC,
∴平面CHI将四棱锥分成四棱锥A-BCHI与多面体HI-ABCD两部分,
过D作DM⊥CH,垂足为M,则A到平面BCHI的距离等于DM,
∵AD⊥平面BCDE,∴AD⊥CD,
在Rt△CDH中,CD=2,DH=1,
CH=![]() ,DM=
,DM=![]() ,
,
∵BC⊥CD,AD⊥BC,AD∩CD=D,
∴BC⊥平面ACD,
∵CH平面ACD,∴BC⊥CH,
四边形BCHI的面积为![]() (1+4)×
(1+4)×![]() =
=![]() ,
,
四棱锥A-BCHI的体积V1=![]() ×
×![]() ×
×![]() =
=![]() ,
,
四棱锥A-BCDE的体积V=![]() ×
×![]() ×(2+4)×2×2=4,
×(2+4)×2×2=4,
多面体HI-ABCD的体积V2=V-V1=![]() ,
,
∴平面CHI将四棱锥A-BCDE分成的两部分体积比为![]() .
.

