题目内容
【题目】定义在R上的奇函数f(x),当x>0时,f(x)=x﹣2
(1)求函数f(x)的解析式;
(2)求不等式f(x)<2的解集.
【答案】
(1)解:由题意知:f(﹣0)=﹣f(0)=f(0),f(0)=0;
当x<0时,则﹣x>0,
因为当x>0时,f(x)=x﹣2,
所以f(﹣x)=﹣x﹣2,
又因为f(x)是定义在R上的奇函数,
所以f(﹣x)=﹣f(x),
所以f(x)=x+2,
所以f(x)的表达式为:f(x)= 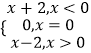
(2)解:x<0时,x+2<2,∴x<0;
x=0,符合题意;
x>0时,x﹣2<2,∴x<4,∴0<x<4.
∴不等式的解集为(﹣∞,4)
【解析】(1)先根据f(x)是定义在R上的奇函数,得到f(0)=0,再设x<0时,则﹣x>0,结合题意得到f(﹣x)=﹣x﹣2,然后利用函数的奇偶性进行化简,进而得到函数的解析式.(2)利用(1)的结论,即可求不等式f(x)<2的解集.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
相关题目
