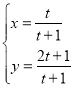Question

【题目】如图，三棱柱ABC﹣A1B1C1中，AA1⊥平面ABC，∠BAC＝90°，AB＝BC＝2，D，E分别为AA1，B1C的中点.

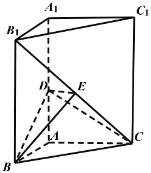
（1）证明：DE⊥平面BCC1B1；

（2）若直线BE与平面AA1B1B所成角为30°，求二面角C﹣BD﹣E的大小.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）取BC的中点F，连结AF，EF，推导出DE∥AF，且DE＝AF，AF⊥BC，由A1A⊥面ABC，且A1A∥B1B，从而B1B⊥面ABC，进而B1B⊥AF，由此能证明AF⊥平面BCC1B1，从而DE⊥面BCC1B.

（2）过F作FH⊥AB，由题意得FH＝1，推导出FH⊥面AA1B1B，即点F到平面AA1B1B的距离为1，EF∥面AA1B1B，E到平面AA1B1B的距离d＝1，求出BE＝2，EF，BB1＝2，以F为原点，FA为x轴，FB为y轴，FE为z轴，建立空间直角坐标系，利用向量法能求出二面角C﹣BD﹣E的大小.

（1）证明：取BC的中点F，连结AF，EF，

则EF∥B1B∥DA，且，

∴DE∥AF，且DE＝AF，又△ABC是等腰直角三角形，

∴AF⊥BC，由A1A⊥面ABC，且A1A∥B1B，∴B1B⊥面ABC，

∴B1B⊥AF，B1B∩BF＝B，∴AF⊥平面BCC1B1，

∴DE⊥面BCC1B.

（2）解：过F作FH⊥AB，由题意得FH＝1，

由A1A⊥面ABC，知A1A⊥面ABC，知A1A⊥FH，

∴FH⊥面AA1B1B，即点F到平面AA1B1B的距离为1，

又EF∥B1B，EF平面AA1B1B，∴EF∥面AA1B1B，

∴点E与点F到平面AA1B1B的距离相等，

∴E到平面AA1B1B的距离d＝1，

∴sin30°，解得BE＝2，∴EF，BB1＝2，

以F为原点，FA为x轴，FB为y轴，FE为z轴，建立空间直角坐标系，

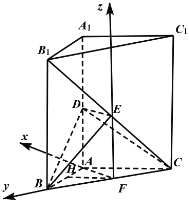
则B（0，，0），C（0，，0），D（），E（0，0，），

∴（0，2，0），（），（0，），

设平面CBD和平面BDE的法向量分别为，（x2，y2，z2），

则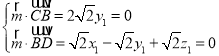，取x1＝1，得（1，0，﹣1），

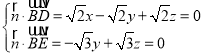，取y2＝1，得（0，1，1），

∴cos，

由图知二面角C﹣BD﹣E是锐二面角，

∴二面角C﹣BD﹣E的大小为.