题目内容
【题目】已知函数fn（x）=a1x+a2x2+a3x3+…+anxn ， 且fn（﹣1）=（﹣1）nn，n∈N* ， 设函数g（n）=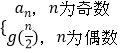 
，若bn=g（2n+4），n∈N* ， 则数列{bn}的前n（n≥2）项和Sn等于 ．
【答案】2n+n﹣1
【解析】解：由函数g（n）=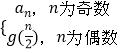 
， 可得bn=g（2n+4）=g（2n﹣1+2）=g（2n﹣2+1）=a 
，
由函数fn（x）=a1x+a2x2+a3x3+…+anxn ， 且fn（﹣1）=（﹣1）nn，
可得﹣a1+a2﹣a3+…+an（﹣1）n=（﹣1）nn，①
n=1时，﹣a1=﹣1，可得a1=1；
n≥2时，﹣a1+a2﹣a3+…+an﹣1（﹣1）n﹣1=（﹣1）n﹣1（n﹣1），②
①﹣②可得an（﹣1）n=（﹣1）nn﹣（﹣1）n﹣1（n﹣1），
化简可得an=2n﹣1，对n=1也成立．
则bn=a =2n﹣1+1，
则数列{bn}的前n（n≥2）项和Sn等于（1+2+4+…+2n﹣1）+n
= 
+n=2n+n﹣1．
故答案为：2n+n﹣1．
由分段函数，求得bn=a ，再由函数fn（x），求得n=1时，a1=1，将n换为n﹣1，作差可得an=2n﹣1，进而得到
bn=2n﹣1+1，再由数列的求和方法：分组求和，结合等比数列的求和公式，计算即可得到所求和．
练习册系列答案
相关题目
