题目内容
15. 如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合).
如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合).(Ⅰ)求证:MN∥BC;
(Ⅱ)求直线AC与平面PBC所成角的大小;
(Ⅲ)若直线EM与直线AP所成角的余弦值$\frac{{3\sqrt{14}}}{14}$时,求MC的长.
分析 (Ⅰ)DE为△ABC的中位线,从而得到DE∥BC,然后根据线面平行的判定定理及性质定理即可得到DE∥MN,从而BC∥MN,即MN∥BC;
(Ⅱ)过B作BZ∥PA,容易说明BC,BA,BZ三条直线互相垂直,从而以B为原点,BC,BA,BZ所在直线为x,y,z轴建立空间直角坐标系,这样即可求得$\overrightarrow{BC},\overrightarrow{BP},\overrightarrow{AC}$的坐标.从而可求出平面PBC的一个法向量坐标$\overrightarrow{n}$,设直线AC与平面PBC所成角为α,根据sinα=$|cos<\overrightarrow{AC},\overrightarrow{n}>|$即可求出α;
(Ⅲ)根据图形设M(0,y,z),由M点在棱BP上,便可得到$\overrightarrow{BM}=λ\overrightarrow{BP}$,从而表示M为M(0,2λ,2λ),根据直线EM与直线AP所成角的余弦值$\frac{{3\sqrt{14}}}{14}$,设直线EM与直线AP所成角为θ,从而通过cosθ=$|\frac{\overrightarrow{EM}•\overrightarrow{AP}}{|\overrightarrow{EM}||\overrightarrow{AP}|}|=\frac{3\sqrt{14}}{14}$即可求出λ,从而求出M点坐标,由两点间距离公式即可求出MC.
解答 解:(Ⅰ)证明:∵D,E分别为AB,AC的中点;
∴DE∥BC,BC?平面PBC,DE?平面PBC;
∴DE∥平面PBC,平面DENM∩平面PBC=MN;
∴DE∥MN;
∴MN∥BC;
(Ⅱ)如图,在平面PAB内作BZ∥PA,则根据: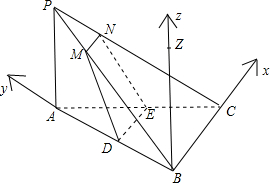
PA⊥底面ABC,及AB⊥BC即知,BC,BA,BZ两两垂直;
∴以B为坐标原点,BC,BA,BZ所在直线为x,y,z轴建立如图所示空间直角坐标系,则:
B(0,0,0),C(2,0,0),A(0,2,0),P(0,2,2);
∴$\overrightarrow{BC}=(2,0,0),\overrightarrow{BP}=(0,2,2)$,$\overrightarrow{AC}=(2,-2,0)$;
设平面PBC的法向量为$\overrightarrow{n}=({x}_{1},{y}_{1},{z}_{1})$;
则由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=0}\\{\overrightarrow{n}•\overrightarrow{BP}=0}\end{array}\right.$得:
$\left\{\begin{array}{l}{2{x}_{1}=0}\\{2{y}_{1}+2{z}_{1}=0}\end{array}\right.$,令z1=1,得x1=0,y1=-1;
∴$\overrightarrow{n}=(0,-1,1)$;
设直线AC和平面PBC所成角为α,则:
sinα=$|cos<\overrightarrow{AC},\overrightarrow{n}>|=|\frac{\overrightarrow{AC}•\overrightarrow{n}}{|\overrightarrow{AC}||\overrightarrow{n}|}|$=$\frac{2}{2\sqrt{2}•\sqrt{2}}=\frac{1}{2}$;
又$α∈[0,\frac{π}{2}]$;
∴$α=\frac{π}{6}$;
即直线AC和平面PBC所成角为$\frac{π}{6}$;
(Ⅲ)设M(0,y,z),M在棱PB上,则:$\overrightarrow{BM}=λ\overrightarrow{BP},(0<λ<1)$;
∴(0,y,z)=λ(0,2,2);
∴M(0,2λ,2λ),E(1,1,0);
∴$\overrightarrow{EM}=(-1,2λ-1,2λ),\overrightarrow{AP}=(0,0,2)$;
因为直线EM与直线AP所成角的余弦值$\frac{{3\sqrt{14}}}{14}$;
设直线EM和直线AP所成角为θ;
所以cosθ=$|\frac{\overrightarrow{EM}•\overrightarrow{AP}}{|\overrightarrow{EM}||\overrightarrow{AP}|}|=\frac{4λ}{\sqrt{8{λ}^{2}-4λ+2}•2}=\frac{3\sqrt{14}}{14}$;
∴8λ2-18λ+9=0;
解得$λ=\frac{3}{4}$,或$λ=\frac{3}{2}$(舍去);
∴M(0,$\frac{3}{2},\frac{3}{2}$);
∴$MC=\sqrt{4+\frac{9}{4}+\frac{9}{4}}=\frac{\sqrt{34}}{2}$.
点评 考查中位线的性质,线面平行的判定定理及性质定理,面面垂直的性质定理,通过建立空间直角坐标系,利用向量解决空间直线与平面,及直线与直线所成角的问题的方法,线面角的定义及范围,以及平面法向量的定义及求平面一个法向量的方法,两向量夹角余弦的坐标公式,两点间的距离公式.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案 有四张卡片,每张卡片有两个面,一个面写有一个数字,另一个面写有一个英文字母.现规定:当卡片的一面为字母P时,它的另一面必须是数字2.如图,下面的四张卡片的一个面分别写有P,Q,2,3,为检验此四张卡片是否有违反规定的写法,则必须翻看的牌是( )
有四张卡片,每张卡片有两个面,一个面写有一个数字,另一个面写有一个英文字母.现规定:当卡片的一面为字母P时,它的另一面必须是数字2.如图,下面的四张卡片的一个面分别写有P,Q,2,3,为检验此四张卡片是否有违反规定的写法,则必须翻看的牌是( )| A. | 第一张,第三张 | B. | 第一张,第四张 | C. | 第二张,第四张 | D. | 第二张,第三张 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1
如图,在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为线段DF上一点.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为线段DF上一点. 已知四棱锥S-ABCD的底面ABCD是正方形,侧棱SC的中点,E在底面内的射影恰好是正方形ABCD的中心O,顶点A在截面ABD内的影射恰好是△SBD的重心G
已知四棱锥S-ABCD的底面ABCD是正方形,侧棱SC的中点,E在底面内的射影恰好是正方形ABCD的中心O,顶点A在截面ABD内的影射恰好是△SBD的重心G