题目内容
20. 已知四棱锥S-ABCD的底面ABCD是正方形,侧棱SC的中点,E在底面内的射影恰好是正方形ABCD的中心O,顶点A在截面ABD内的影射恰好是△SBD的重心G
已知四棱锥S-ABCD的底面ABCD是正方形,侧棱SC的中点,E在底面内的射影恰好是正方形ABCD的中心O,顶点A在截面ABD内的影射恰好是△SBD的重心G(Ⅰ)求证:△SBD是等边三角形;
(Ⅱ)设AB=a,求二面角B-SD-C余弦值的大小.
分析 (Ⅰ)根据条件证明G是△SBD的垂心,即可证明△SBD是等边三角形;
(Ⅱ)设AB=a,建立直角坐标系,求平面的法向量,利用向量法即可求二面角B-SD-C余弦值的大小.
解答 证明:(Ⅰ)∵O,E分别是AC,SC的中点,
∴SA∥OE.
∵底面ABCD是正方形,
∴SA,AB,AD两两垂直,连接DG并延长交SB于F,
∵SO是△SBD的直线,
∴G在SO上,
∵AG⊥平面SBD,
∴AG⊥SB,
∵AD⊥SB,
∴SB⊥平面ADF,
同理SO⊥BD,BG⊥SD,
则G是△SBD的垂心,
∵G是△SBD的重心,
∴△SBD是等边三角形;
(Ⅱ)由(Ⅰ)知,SA,AB,AD两两垂直,且SA=AB=AD,
建立如图所示的直角坐标系,
设AB=a,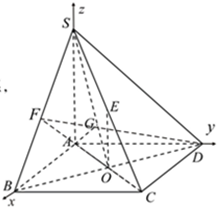
则B(-a,0,a),C(a,a,0),
D(0,a,0),S(0,0,a),
则$\overrightarrow{BS}$=(-a,0,a),$\overrightarrow{BD}$=(-a,a,0),
设平面SBD的一个法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{BS}•\overrightarrow{m}=-ax+az=0}\\{\overrightarrow{BD}•\overrightarrow{m}=-ax+ay=0}\end{array}\right.$,
令x=1,则y=1,z=1,
即为$\overrightarrow{m}$=(1,1,1),
同理平面SCD的一个法向量为$\overrightarrow{n}$=(0,1,1)
∵cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1+1}{\sqrt{3}×\sqrt{2}}$=$\frac{\sqrt{6}}{3}$,
∴二面角B-SD-C余弦值的大小为$\frac{\sqrt{6}}{3}$.
点评 本题主要考查二面角的求解,建立坐标系,利用向量法是解决线面所成角的常用方法.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$. 如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合).
如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合). 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.