题目内容
不等式(a-3)x2<(4a-2)x对a∈(0,1)恒成立,则x的取值范围是______.
令g(a)=(x2-4x)a-3x2+2x,a∈(0,1)
由题意可得g(a)<0在a∈(0,1)恒成立,结合一次函数的单调性可得
即
解不等式可得x<-1或x>
故答案为:{x|x<-1或x>
}
由题意可得g(a)<0在a∈(0,1)恒成立,结合一次函数的单调性可得
|
|
解不等式可得x<-1或x>
| 2 |
| 3 |
故答案为:{x|x<-1或x>
| 2 |
| 3 |

练习册系列答案
相关题目
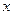 的不等式
的不等式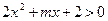
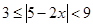 的解集为 .
的解集为 .