题目内容
设集合A={x|x2+2x-3>0},集合B={x|x2-ax-1≤0,a>0},若A∩B中恰含有一个整数,则实数a的取值范围是( )
A.(0,
| B.[
| C.[
| D.(2,+∞) |
A={x|x2+2x-3>0}={x|x>1或x<-3},
设f(x)=x2-ax-1,则f(0)=-1<0,对称轴x=-
=
>0,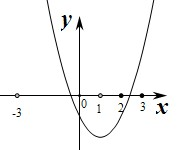
∴要使A∩B中恰含有一个整数,
则
,
即
,
∴
,即
≤a<
,
∴实数a的取值范围是[
,
).
故选:B
设f(x)=x2-ax-1,则f(0)=-1<0,对称轴x=-
| -a |
| 2 |
| a |
| 2 |

∴要使A∩B中恰含有一个整数,
则
|
即
|
∴
|
| 3 |
| 2 |
| 8 |
| 3 |
∴实数a的取值范围是[
| 3 |
| 2 |
| 8 |
| 3 |
故选:B

练习册系列答案
相关题目
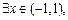 使不等式
使不等式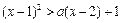 成立;命题q:
成立;命题q: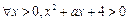 恒成立.已知p或q为真,求实数a的取值范围.
恒成立.已知p或q为真,求实数a的取值范围.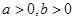 ,且
,且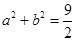 ,若
,若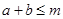 恒成立.
恒成立.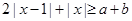 对任意的
对任意的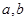 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.