题目内容

解不等式：
（1）x2+2x-35≤0
（2）2x2+5x+4＜0
（3）-3x2+5x-2＞0
（4）-x2+x-
1
4
≤0．
（1）由x2-2x-35≤0，化为（x-7）（x+5）≤0，∴-5≤x≤7，因此原不等式的解集为{x|-5≤x≤7}；
（2）∵△=52-2×4×4=-7＜0，∴2x2+5x+4＜0的解集是∅；
（3）-3x2+5x-2＞0化为3x2-5x+2＜0，∴（3x-2）（x-1）＜0，∴
2
3
＜x＜1，因此原不等式的解集为{x|
2
3
＜x＜1}；
（4）-x2+x-
1
4
≤0化为x2-x+
1
4
≥0，即(x-
1
2
)2≥0，因此不等式的解集为R．
练习册系列答案
相关题目
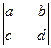若规定=|ad－bc|，则不等式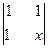<2的解集为           ．
已知mx2+mx+m＜1的解集为R，则m的取值范围是（　　）
A．（-∞，0）B．(-∞，0)∪(
4
3
，+∞)		C．（-∞，0]D．(-∞，0]∪[
4
3
，+∞)
不等式x（x-2）≤0的解集是（　　）
A．[0，2）B．[0，2]C．（-∞，0]∪[2，+∞）D．（-∞，0）∪（2，+∞）
若不等式
1
p
x2+qx+p＞0的解集为{x|2＜x＜4}，则实数p=______．
已知不等式x2+bx+c＞0的解集为{|x|x＞2或x＜1}，则不等式cx2+bx+1≤0的解集为（　　）
A．{x|
1
2
≤x≤1}		B．{x|-1≤x≤-
1
2
}
C．{x|x≥1，或x≤
1
2
}		D．∅
不等式（a-3）x2＜（4a-2）x对a∈（0，1）恒成立，则x的取值范围是______．
若不等式ax2+bx-2＞0的解集为{x丨1＜x＜2}，则实数a，b的值为（　　）
A．a=1，b=3B．a=-1，b=3C．a=-1，b=-3D．a=1，b=-3
不等式|2-x|+|x+1|≤a对任意x∈[0，5]恒成立的实数a的取值范围是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网