题目内容
2.已知函数f(x)=a${\;}^{1+\sqrt{1-{x}^{2}}}$+b(a>0且a≠1)最大值为4,最小值为2,求实数a与b的值.分析 通过题意易知1+$\sqrt{1-{x}^{2}}$∈[1,2],分0<a<1、a>1两种情况讨论即可.
解答 解:依题意可知$\sqrt{1-{x}^{2}}$∈[0,1],
∴1+$\sqrt{1-{x}^{2}}$∈[1,2],
①当0<a<1时,y=ax为减函数,
∴$\left\{\begin{array}{l}{a+b=4}\\{{a}^{2}+b=2}\end{array}\right.$,显然无解;
②当a>1时,y=ax为增函数,
∴$\left\{\begin{array}{l}{a+b=2}\\{{a}^{2}+b=4}\end{array}\right.$,
两式相减得:a2-a-2=0,
∴(a-2)(a+1)=0,
解得:a=2或a=-1(舍),
∴b=2-a=2-2=0;
综上所述,a=2,b=0.
点评 本题考查函数的单调性,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
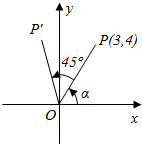 如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.
如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.