题目内容
5.在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{A{{\;}_{1}B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则$\overrightarrow{{B_1}M}$=$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)分析 根据题意,画出图形,结合图形,利用向量的加法几何意义表示出$\overrightarrow{{B}_{1}B}$、$\overrightarrow{BM}$,从而得出$\overrightarrow{{B_1}M}$.
解答 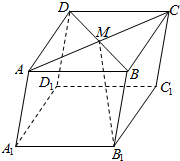 解:如图所示,
解:如图所示,
平行六面体ABCD-A1B1C1D1中,
M为AC与BD的交点,$\overrightarrow{A{{\;}_{1}B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,
∴$\overrightarrow{{B}_{1}B}$=$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,
$\overrightarrow{BM}$=$\frac{1}{2}$$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)=$\frac{1}{2}$($\overrightarrow{{{B}_{1}A}_{1}}$+$\overrightarrow{{{B}_{1}C}_{1}}$)=$\frac{1}{2}$(-$\overrightarrow{{{A}_{1}B}_{1}}$+$\overrightarrow{{{A}_{1}D}_{1}}$)=$\frac{1}{2}$(-$\overrightarrow{a}$+$\overrightarrow{b}$);
∴$\overrightarrow{{B_1}M}$=$\overrightarrow{{B}_{1}B}$+$\overrightarrow{BM}$=$\overrightarrow{c}$+$\frac{1}{2}$(-$\overrightarrow{a}$+$\overrightarrow{b}$)=$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.
故答案为:$\overrightarrow c+\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$.
点评 本题考查了空间向量的加法运算的几何意义,也考查了空间想象能力,是基础题目.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
| A. | 1 | B. | 3 | C. | 4 | D. | -2 |
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |