题目内容
已知数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, .
.
(Ⅰ)问:数列 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(Ⅱ)求 和
和 ;
;
(Ⅲ)求证: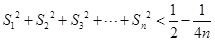 .
.
 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, .
.(Ⅰ)问:数列
 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;(Ⅱ)求
 和
和 ;
;(Ⅲ)求证:
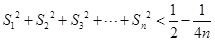 .
.(1)见解析;(2)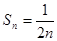 ,
,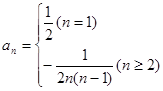 ;(3)见解析.
;(3)见解析.
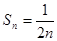 ,
,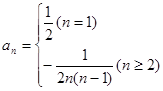 ;(3)见解析.
;(3)见解析.本题主要考查递推数列、等差数列与不等式的综合应用,考查分类讨论思想,考查放缩的方法
解:(1)由已知有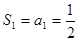 ,
,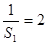 ;
; 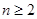 时,
时,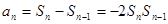
所以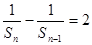 ,即
,即 是以2为首项,公差为2 的等差数列.
是以2为首项,公差为2 的等差数列.
(2)由(1)得: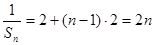 ,
,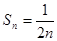
当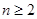 时,
时,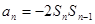
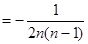 .
.
当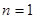 时,
时,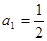 ,所以
,所以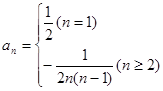
(3)当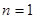 时,
时,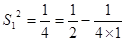 ,成立.
,成立.
当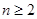 时,
时,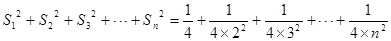
=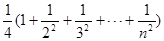
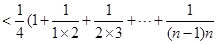
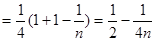 综上有
综上有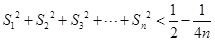 .
.
解:(1)由已知有
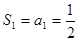 ,
,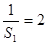 ;
; 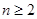 时,
时,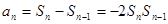
所以
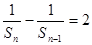 ,即
,即 是以2为首项,公差为2 的等差数列.
是以2为首项,公差为2 的等差数列.(2)由(1)得:
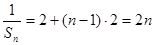 ,
,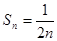
当
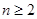 时,
时,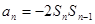
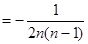 .
.当
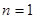 时,
时,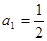 ,所以
,所以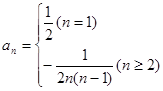
(3)当
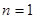 时,
时,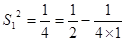 ,成立.
,成立.当
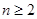 时,
时,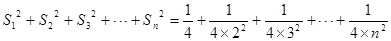
=
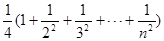
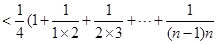
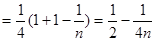 综上有
综上有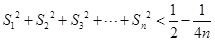 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 ,34,…中,
,34,…中,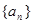 满足
满足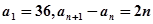 ,则
,则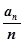 的最小值是 .
的最小值是 . 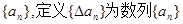 的一阶差分数列,其中
的一阶差分数列,其中 若数列{
若数列{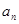 }的通项公式
}的通项公式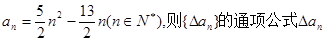 ="________."
="________."  中,
中,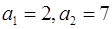 且
且  ,则
,则 等于
等于 ,则其前n项的和等于 。
,则其前n项的和等于 。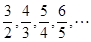 那么它的一个通项公式是( )
那么它的一个通项公式是( )



 中,
中, ,则
,则 =( )
=( )


