题目内容
6. 如图,在△ABC中,∠A=60°,AB=2AC=8,过C作△ABC外接圆的切线CD,BD⊥CD于D,BD与外接圆交于点E,则DE=2.
如图,在△ABC中,∠A=60°,AB=2AC=8,过C作△ABC外接圆的切线CD,BD⊥CD于D,BD与外接圆交于点E,则DE=2.
分析 利用直角△ABC的边角关系即可得出BC,利用弦切角定理可得∠BCD=∠A=60°.利用直角△BCD的边角关系即可得出CD,BD.再利用切割线定理可得CD2=DE•DB,即可得出DE.
解答 解:在△ABC中,∠C=90°,∠A=60°,AB=8,∴BC=AB•sin60°=4$\sqrt{3}$.
∵CD是此圆的切线,∴∠BCD=∠A=60°.
在Rt△BCD中,CD=BC•cos60°=2$\sqrt{3}$,BD=BC•sin60°=6.
由切割线定理可得CD2=DE•DB,∴12=6DE,解得DE=2.
故答案为:2.
点评 熟练掌握直角三角形的边角关系、弦切角定理、切割线定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.若一球的表面积为8π,则它的体积为( )
| A. | $\frac{4\sqrt{2}π}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$ | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |
5.如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为( )


| A. | 相交 | B. | 平行 | C. | 异面而且垂直 | D. | 异面但不垂直 |
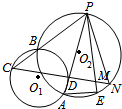 如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.
如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N. 如图,已知正三棱柱ABC-A1B1C1所有棱长均为a,D为BB1上一点,则三棱锥C1-ACD的体积为$\frac{{\sqrt{3}}}{12}{a^3}$.
如图,已知正三棱柱ABC-A1B1C1所有棱长均为a,D为BB1上一点,则三棱锥C1-ACD的体积为$\frac{{\sqrt{3}}}{12}{a^3}$. 已知BC为圆O的直径,点A为圆周上一点,AD⊥BC于点D,过点A作圆O的切线交BC的延长线于点P,过点B作BE垂直PA的延长线于点E.求证:
已知BC为圆O的直径,点A为圆周上一点,AD⊥BC于点D,过点A作圆O的切线交BC的延长线于点P,过点B作BE垂直PA的延长线于点E.求证: