题目内容

1．如图，已知正三棱柱ABC-A1B1C1所有棱长均为a，D为BB1上一点，则三棱锥C1-ACD的体积为$\frac{{\sqrt{3}}}{12}{a^3}$．

分析 如图所示，取AC的中点E，连接BE，由△ABC是等边三角形，可得BE⊥AC，利用面面垂直的性质可得：BE⊥平面侧面ACC1A1，再利用三棱锥C1-ACD的体积V=${V}_{三棱锥D-AC{C}_{1}}$=$\frac{1}{3}×BE•{S}_{△AC{C}_{1}}$，即可得出．

解答 解：如图所示，取AC的中点E，连接BE，
∵△ABC是等边三角形，
∴BE⊥AC，
由正三棱柱ABC-A1B1C1，可得侧面ACC1A1⊥底面ABC，侧面ACC1A1∩底面ABC，
∴BE⊥平面侧面ACC1A1，
${S}_{△AC{C}_{1}}$=$\frac{1}{2}AC•C{C}_{1}$-$\frac{1}{2}×{a}^{2}$．
∴三棱锥C1-ACD的体积V=${V}_{三棱锥D-AC{C}_{1}}$=$\frac{1}{3}×BE•{S}_{△AC{C}_{1}}$=$\frac{1}{3}×\frac{\sqrt{3}}{2}a×\frac{1}{2}{a}^{2}$=$\frac{{\sqrt{3}}}{12}{a^3}$．
故答案为：$\frac{{\sqrt{3}}}{12}{a^3}$．

点评 本题考查了面面垂直的性质、三棱锥的体积计算公式、等边三角形的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
6．若在区间（a，b）上任意x满足f（x）＞0，f′（x）＞0，f″（x）＞0，其中f′（x）为f（x）的导数，f″（x）是f′（x）的导数，则称f（x）是区间（a，b）上的“δ”函数．已知函数φ（x）=$\frac{m}{3}$x3-$\frac{1}{2}$x2-x+ex是区间（0，+∞）上的“δ”函数．
（1）实数m的取值范围是m＞-$\frac{1}{2}$；
（2）若g（x）=$\frac{1}{3}$x3-$\frac{1}{2}$x2-x+ex，记S1=${∫}_{a}^{b}$g（x）dx，S2=$\frac{g（a）+g（b）}{2}$•（b-a），S3=g（a）（b-a），其中b＞a＞0，则S1，S2，S3中最大的为s2＞s1＞s3．
12．在空间中，下列结论正确的是（　　）
A．平行于同一直线的两直线平行B．垂直于同一直线的两直线平行
C．平行于同一平面的两直线平行D．垂直于同一平面的两直线垂直
9．已知函数f（x）=$\frac{ax+b}{x}{e^x}$，a，b∈R，且a＞0
（1）当a=2，b=1，求函数f（x）的极值；
（2）设g（x）=a（x-1）ex-f（x），若存在x＞1，使得g（x）+g′（x）=0成立，求$\frac{b}{a}$的取值范围．
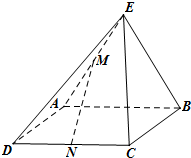16．如图，矩形ABCD所在平面与直角三角形ABE所在平面互相垂直，AE⊥BE，点M，N分别是AE，CD的中点．
（1）求证：MN∥平面BCE；
（2）求证：平面BCE⊥平面ADE．
6．如图，在△ABC中，∠A=60°，AB=2AC=8，过C作△ABC外接圆的切线CD，BD⊥CD于D，BD与外接圆交于点E，则DE=2．
13．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M，T（不与A，B重合），连结MC，MB，OT．
（Ⅰ）求证：MTCO四点共圆；
（Ⅱ）求证：MD=2MC．
10．已知各项都为正数的数列{an}的前n项和为Sn，且4Sn=（an+1）2．
（1）求证：数列{an}为等差数列；
（2）已知数列{bn}满足：b1=2，bn+1=bn+$\frac{{a}_{n}}{{2}^{n}}$，求数列{bn}的通项公式；
（3）设cn=$\frac{n}{（{a}_{n}{a}_{n+1}）^{2}}$，记数列{cn}的前n项和为Tn，如果对于任意的n∈N*，不等式λTn＜$\frac{n+1}{2n+1}$[n+18（-1）n+1]都成立，求实数λ的取值范围．
20．已知函数f（x）=$\frac{{2}^{x}+a}{{2}^{x}-a}$（a∈R）．
（1）若函数f（x）为奇函数，求a的值；
（2）当a=-1，若不等式f（k-t2）+f（|2t-1|）＜0对于任意的t∈[-3，2]恒成立，求实数k的取值范围；
（3）当a≠0时，存在区间[m，n]，使得函数f（x）在[m，n]的值域为[2m，2n]，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网