题目内容
2.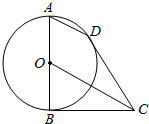 如图所示,AB为圆O的直径,CB,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,CB,CD为圆O的切线,B,D为切点.(1)求证:AD∥OC;
(2)若圆O的半径为2,求AD•OC的值.
分析 (1)连接BD,OD,利用切线的性质,证明BD⊥OC,利用AB为直径,证明AD⊥DB,即可证明AD∥OC;
(2)证明Rt△BAD∽Rt△COB,可得$\frac{AD}{OB}=\frac{AB}{OC}$,即可求AD•OC的值
解答  (1)证明:连接BD,OD,
(1)证明:连接BD,OD,
∵CB,CD是圆O的两条切线,
∴BD⊥OC,
又AB为直径,∴AD⊥DB,
∴AD∥OC.(5分)
(2)解:∵AD∥OC,∴∠DAB=∠COB,
∴Rt△BAD∽Rt△COB,
∴$\frac{AD}{OB}=\frac{AB}{OC}$,
∴AD•OC=AB•OB=8.(10分)
点评 本小题主要考查平面几何的证明,具体涉及到圆的切线的性质,三角形相似等内容.本小题重点考查考生对平面几何推理能力.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
13.在△ABC中,角A,B,C所对应的边分别为a,b,c.若a=$\sqrt{2}$,b=2,B=$\frac{π}{4}$,则A的值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
10.一个圆锥的体积是$\frac{π}{3}$,高是1,它的顶点和底面圆周在球O的球面上,则球O的表面积是( )
| A. | π | B. | 2π | C. | 4π | D. | 8π |
12.当n=3时,执行如图所示的程序框图,输出的S值为( )
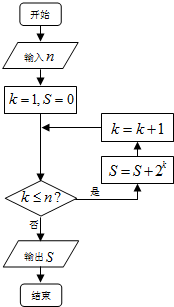

| A. | 30 | B. | 14 | C. | 8 | D. | 6 |
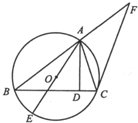 如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.
如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.