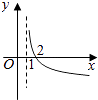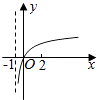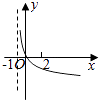题目内容
【题目】设函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 的单调递增区间及对称中心;
的单调递增区间及对称中心;
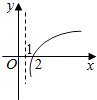
(3)函数![]() 可以由
可以由![]() 经过怎样的变换得到.
经过怎样的变换得到.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)见解析.
;(3)见解析.
【解析】
分析:根据正弦的两角和公式与辅助角公式将![]() 化简为
化简为![]() 或
或![]() .
.
. (1)结合最小正周期计算公式![]() ,得最小正周期;
,得最小正周期;
(2)解法一:利用余弦函数单调性解不等式,可得函数![]() 的递增区间;再由余弦函数的对称中心解方程,可得函数
的递增区间;再由余弦函数的对称中心解方程,可得函数![]() 的对称中心;
的对称中心;
解法二:利用正弦函数单调性解不等式,可得函数![]() 的递增区间;再由正弦函数的对称中心解方程,可得函数
的递增区间;再由正弦函数的对称中心解方程,可得函数![]() 的对称中心;
的对称中心;
(3)解法一:将函数![]() 的图象向右平移
的图象向右平移![]() ,横坐标压缩到原来的
,横坐标压缩到原来的![]() ,纵坐标拉伸到原来的2倍,即可得到函数
,纵坐标拉伸到原来的2倍,即可得到函数![]() 的图象.
的图象.
解法二:将函数![]() 的图象向右平移
的图象向右平移![]() ,横坐标压缩到原来的
,横坐标压缩到原来的![]() ,纵坐标拉伸到原来的2倍,即可得到函数
,纵坐标拉伸到原来的2倍,即可得到函数![]() 的图象.
的图象.
详解:解:解法一
因为![]() ,
,
所以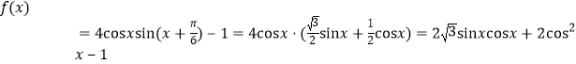
![]() .
.
(1)因为![]() , 所以
, 所以![]() .
.
(2)由![]() ,
,
所以函数的单调递增区间为:![]() ,
,
由![]() ,
,
所以对称中心为:![]() .
.
(3)函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象
的图象
函数![]() 的图象上的每一点的纵坐标不变,横坐标变为原来的
的图象上的每一点的纵坐标不变,横坐标变为原来的![]() ,得到函数
,得到函数![]()
函数![]() 的图象上的每一点的横坐标不变,纵坐标变为原来的倍2
的图象上的每一点的横坐标不变,纵坐标变为原来的倍2
得到函数![]() 的图象.
的图象.
解法二
因为![]() ,
,
所以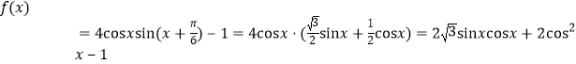 ,
,
![]()
(1)因为![]() , 所以
, 所以![]()
(2)由![]()
所以函数的单调递增区间为:![]()
由![]() ,
,
所以对称中心为:![]() .
.
(3)函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象
的图象
函数![]() 的图象上的每一点的纵坐标不变,横坐标变为原来的
的图象上的每一点的纵坐标不变,横坐标变为原来的![]() ,
,
得到函数![]() 。
。
函数![]() 的图象上的每一点的横坐标不变,纵坐标变为原来的倍2,
的图象上的每一点的横坐标不变,纵坐标变为原来的倍2,
得到函数![]() 的图象.
的图象.

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)的影响,对近六年的年宣传费
(单位:吨)的影响,对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣传费 | 23 | 25 | 27 | 29 | 32 | 35 |
年销售量 | 11 | 21 | 24 | 66 | 115 | 325 |
(1)根据散点图判断![]() 与
与![]() ,哪一个更适合作为年销售量
,哪一个更适合作为年销售量![]() (吨)与关于宣传费
(吨)与关于宣传费![]() (万元)的回归方程类型;
(万元)的回归方程类型;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为
(万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为![]() ,试求
,试求![]() 的所有取值情况及对应的概率;
的所有取值情况及对应的概率;
(3)根据频率分布直方图中求出样本数据平均数的思想方法,求![]() 的平均数.
的平均数.