题目内容
已知关于x的二次函数f（x）=x2+（2t-1）x+1-2t，（1）求证：对于任意t∈R，方程f（x）=1必有实数根；
（2）若
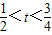，求证：方程f（x）=0在区间
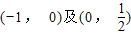上各有一个实数根．
【答案】分析：（1）求证：对于任意t∈R，方程f（x）=1必有实数根；只需找出一个实根即可，也可以用判别式来解．
（2）计算x=-1、0、
时的函数值即可证明要求证的问题．
解答：解：（1）由f（1）=1知f（x）=1必有实数根，
或由△=（2t-1）2+8t=（2t+1）2≥0得f（x）=1必有实数根；
（2）当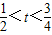
时，
因为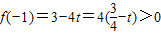
，
，
，
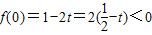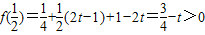所以方程f（x）=0在区间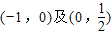
上各有一个实数根．
点评：本题考查根的存在性及根的个数问题，是基础题．
（2）计算x=-1、0、
时的函数值即可证明要求证的问题．解答：解：（1）由f（1）=1知f（x）=1必有实数根，
或由△=（2t-1）2+8t=（2t+1）2≥0得f（x）=1必有实数根；
（2）当
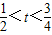时，因为
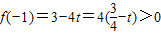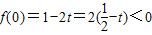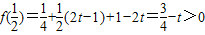，，，所以方程f（x）=0在区间
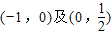上各有一个实数根．点评：本题考查根的存在性及根的个数问题，是基础题．
练习册系列答案
相关题目
已知关于x的二次函数f（x）=x2+ax-b（a，b∈R）．