题目内容

已知关于x的二次函数f（x）=ax2-2bx-1，（其中常数a、b∈R），满足
a+b-6≤0
a＞0
b＞0
，则函数y=f（x）在区间[2，+∞）上是增函数的概率是（　　）
A、
1
4
B、
1
3
C、
1
2
D、
2
3
分析：先算出函数y=f（x）在区间[2，+∞）上是增函数的充要条件，将a，b看成未知数，利用画平面区域的方法结合几何概型解决问题．
解答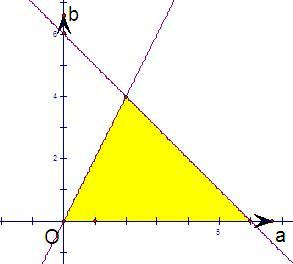：精英家教网解：函数y=f（x）在区间[2，+∞）上是增函数的充要条件是：
a＞0
b≤ 2a
，画出满足
a+b-6≤0
a＞0
b＞0
，
和
a＞0
b≤ 2a
，的平面区域：
∴是增函数的概率=
阴影部分的面积
大三角形的面积
=
2
3
．
故选D．
点评：本题主要考查了简单的线性规划，以及利用几何概型求概率的方法，属于基础题．
练习册系列答案
相关题目
已知关于x的二次函数f（x）=x2+（2t-1）x+1-2t．
（1）求证：对于任意t∈R，方程f（x）=1必有实数根；
（2）若方程f（x）=0在区间（-1，2）上有两个实数根，求t的范围．
精英家教网已知关于x的二次函数f（x）=x2+ax-b（a，b∈R）．
（Ⅰ）当b=-2时，由于对任意的x∈R，函数f（x）的值总大于零，求实数a的取值范围；
（Ⅱ）如果方程f（x）=0有一个负根和一个不大于1的正根，求实数a，b满足的条件，并在右图所给坐标系中画出点（a，b）所在的平面区域；
（Ⅲ）在第（Ⅱ）问的条件下，若实数k满足b=k（a+1）+3，求k的取值范围．
已知关于x的二次函数f（x）=ax2-8bx+1．
（1）设集合M={1，2，3}和N={-1，1，2，3，4，5}，从集合M中随机取一个数作为a，从N中随机取一个数作为b，求函数y=f（x）在区间[2，+∞）上是增函数的概率；
（2）设点（a，b）是区域
x+y-6≤0
x＞0
y＞0
内的随机点，求函数y=f（x）在区间[2，+∞）上是增函数的概率．
已知关于x的二次函数f（x）=ax2-4bx+1
（Ⅰ）设集合P={1，2，3}，集合Q={-1，1，2，3，4}，从集合P中随机取一个数作为a，从集合Q中随机取一个数作为b，求函数f（x）在区间[1，+∞）上是增函数的概率；
（Ⅱ）设点（a，b）是区域
x+y-8≤0
x＞0
y＞0
内的随机点，求函数f（x）在区间[1，+∞）上是增函数的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网